摘要
为了快速、可靠、准确地评价边坡稳定性,提出了一种基于优化算法优化 BP神经网络的边坡稳定性预测方法,该方法可以通过基本的几何、地质因素客观地评价边坡稳定性,克服了传统机器学习模型选择困难和误判风险高的缺点。收集505组边坡样本,将优化算法优化的BP神经网络预测模型与常用的学习模型进行预测性能比较。研究结果表明:基于同样的数据集,思维进化算法(MEA)优化BP神经网络模型泛化性能最佳。MEA-BP神经网络模型能够有效地预测边坡的稳定性,精确率P为0. 903,ROC曲线线下面积 (AUC)为0. 93,在预测的准确性及泛化能力上明显优于BP神经网络,基于MEA-BP的方法有望成为边坡稳定性预测的通用方法。
Abstract
In order to quickly, reliably, and accurately evaluate slope stability, a slope stability prediction method based on optimization algorithm optimized BP neural network is proposed. This method can objectively evaluate slope stability through basic geometric and geological factors, overcoming the shortcomings of traditional machine learning model selection difficulties and high risk of misjudgment. Collect 505 sets of slope samples and compare the prediction performance of the optimized BP neural network prediction model with commonly used learning models. The research results indicate that based on the same dataset, the Mind Evolutionary Algorithm (MEA) optimizes the generalization performance of the BP neural network model with the best performance. The MEA-BP neural network model can effectively predict the stability of slopes with an accuracy rate of P of 0. 903 and an area below the ROC curve (AUC) of 0. 93. It is significantly superior to the BP neural network in terms of prediction accuracy and generalization ability. The method based on MEA-BP is expected to become a common method for predicting slope stability.
Keywords
0 引言
滑坡是地质灾害中的一种主要类型,关于滑坡的危险性评价国内外有许多研究成果。然而,不同的研究方法和评价标准存在差异(Fausto et al., 1999)。目前边坡稳定性的评价方法有极限平衡法 (Kang et al.,2013)、数值分析法(黄林,2020)和监测预警法(Chen et al.,2018)等。各种方法各有优缺点,例如极限平衡法具有明确的物理意义,但存在确定临界滑移面困难和依赖简化假设的问题 (Kang et al.,2013);数值计算方法可以模拟边坡破坏全过程,得出位移场、应力场和渗流场,但可靠性受岩土体强度参数和本构模型影响较大(Qi and Tang,2018);监测预警方法是减少滑坡和边坡失稳灾害的有效途径,但面临选取预警指标困难和大量监测数据导致时效性不足的挑战(Dick et al., 2015)。
随着科学技术的进一步发展,数学模型和机器学习算法在工程领域得到了广泛的应用(邵勇等, 2020;李明亮等,2021;赵泽宁等,2021)。其中,数据驱动的方法通过分析样本数据,可以发现其中的规律。这种方法具有很强的客观性,并且无需收集具体物理模型所需的参数,能够快速、广泛地评估边坡的稳定性(Aleotti and Chowdhury,1999)。考虑到边坡灾害的复杂性,近年来数据驱动的方法受到越来越多研究的重视,例如使用支持向量机等机器学习模型(管新邦,2018)。
本文通过全面提取和筛选滑坡的特征,采用优化算法和神经网络方法构建了边坡稳定性评价模型,并在三峡库区边坡进行了验证。该模型评价结果可为滑坡灾害的预防和治理提供参考依据。
1 数据与方法
1.1 边坡稳定性评价的模型算法
1.1.1 BP神经网络
BP神经网络是一种常见的人工神经网络,也是一种有监督学习算法。它的输入层、隐含层和输出层都由多个神经元节点组成,网络拓扑结构如图1所示。
1.1.2 基于思维进化算法优化的BP神经网络
孙承意等(1999)在遗传算法的基础上提出了思维进化算法,对“趋同”和“异化”进行探测和开发,从而有效解决了遗传算法收敛效率低等缺点。本文使用MEA的优化思路如下:

图1神经网络拓扑结构
(1)选择数据集。本文将数据集按照 7∶3 的比例分为训练集和预测集;
(2)生成初始种群;
(3)种群趋同操作。采用收敛运算和竞争机制的中心思想,通过逐步优化每个子种群的个体,找到局部最优解并提高整体解决方案的质量;
(4)子种群异化;
(5)分析最优个体。
通过迭代操作和解码规则,找到最优个体,并将其权重和阈值应用于神经网络。该方法的目标是通过优化网络参数来获得一个成熟的 BP 神经网络,MEA-BP 神经网络算法的结构示意图如图2所示。
1.1.3 基于遗传算法优化的BP神经网络
遗传算法(GA)是由美国学者Holland J. 提出的一种基于自然进化理论而演化形成的随机并行优化方法(徐磊,2007)。遗传算法具有简单、并行性、耐噪音性和鲁棒性等优点。
本文以建立的神经网络模型为适应度函数,使用二进制编码的方法,将待优化的参数进行编码,编码后的参数称为染色体。调用构建好的 BP 神经网络,进行选择、交叉、变异等操作,搜寻最优的染色体(问题的最优解)。GA优化BP神经网络主要分为 BP 神经网络拓扑结构的确定、GA 优化初始权重和阈值、BP 神经网络训练和预测共 4 个部分(刘奕君等,2015)。
1.1.4 基于麻雀搜索算法优化的BP神经网络
Xue and Shen(2020)模仿麻雀群的觅食和反捕食行为,提出了新型群智能优化算法麻雀搜索算法(SSA),SSA 具有搜索精度高、收敛快、稳定性好和鲁棒性强等特点。

图2MEA-BP神经网络算法的结构示意图
1.2 模型评估
根据分类任务,真实标签和预测标签分为4种:真正例(TP)、假正例(FP)、真负例(TN)、假负例 (FN),4 项的和为样本总数,分类结果构成混淆矩阵(表1)。
表1分类结果混淆矩阵
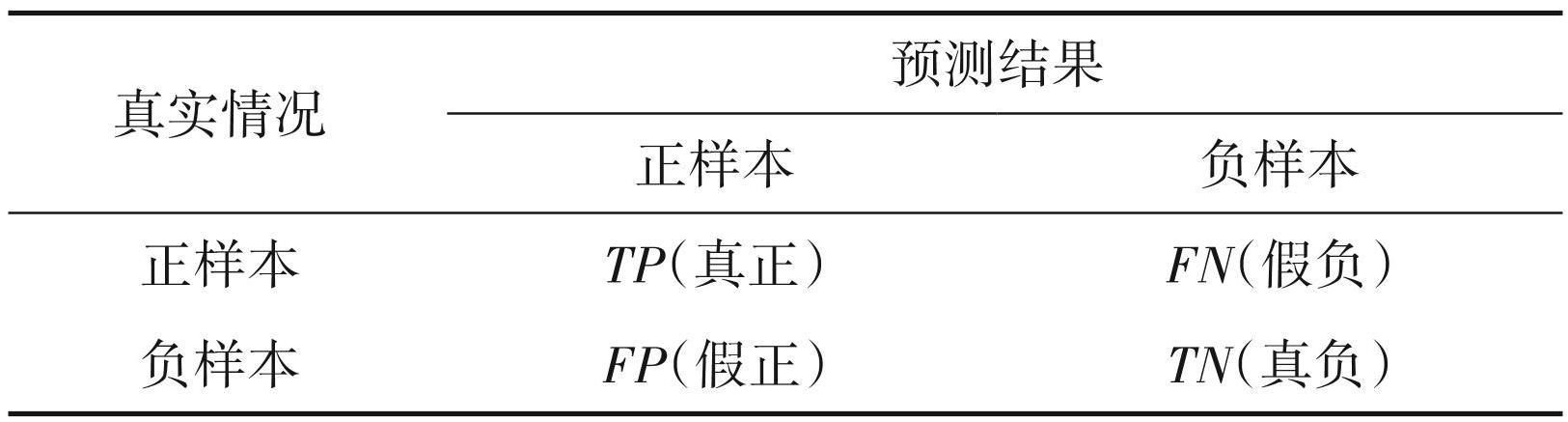
本文主要介绍了3个评估指标,分别是精确率、召回率和F1-score。
(1)精确率(P):分类正确的正样本个数(TP)占判定为正样本的个数(TP+FP)的比例,定义式如下:
(1)
(2)召回率(R):分类正确的正样本个数(TP)占真正的正样本个数(TP+FN)的比例,定义式如下:
(2)
(3)平衡 F 分数:P 与 R 的调和平均数,定义式如下:
(3)
(4)AUC(曲线下面积)是衡量受试者工作特征曲线(简称 ROC 曲线)的性能的一种指标。在每次预测中,计算真正率(TPR)和假正率(FPR),如式 (4)和式(5)所示,并将它们作为ROC曲线的纵坐标和横坐标。
(4)
(5)
AUC 的取值范围是 0~1,越高表示模型的性能越好。利用 AUC 可以比较不同模型之间的优劣以及选择最优模型进行分类任务。
1.3 数据收集与处理
收集与边坡稳定性相关的数据,包括边坡的地质、地形、水文等信息,以及边坡发生滑坡的历史记录。
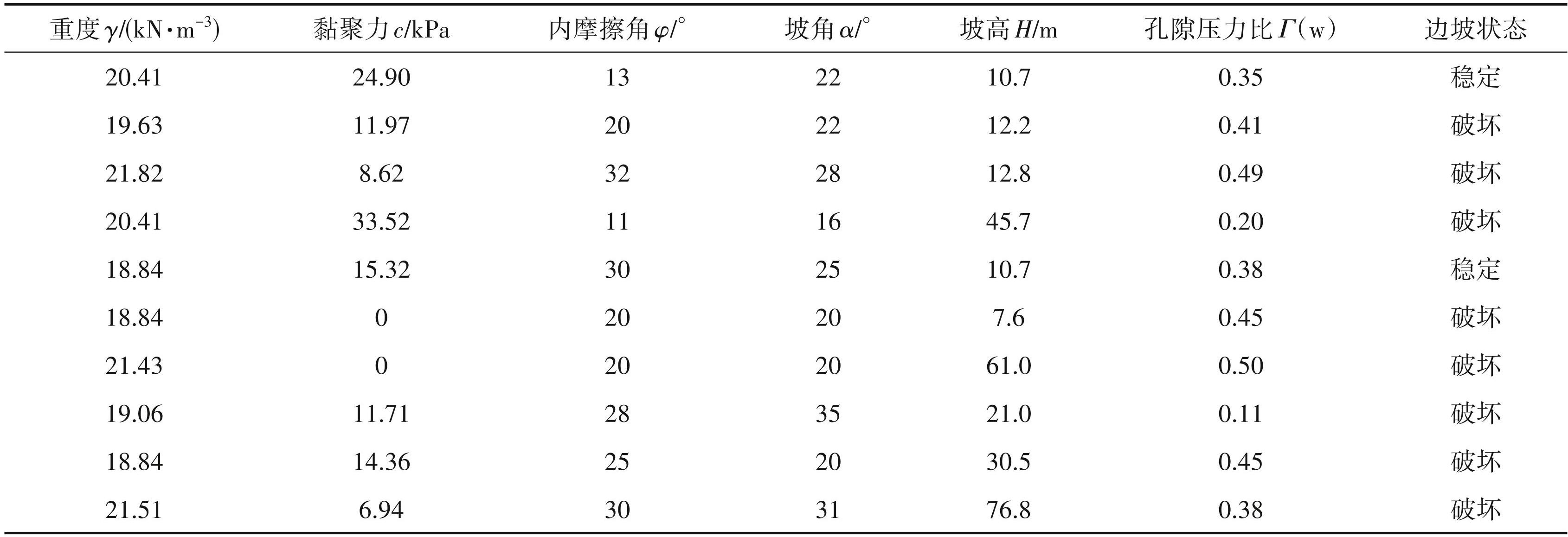
边坡稳定性受到多种因素的影响,根据王超 (2009)预测指标选择方案与结果,边坡稳定性评价选择具有代表性的反映岩体强度、地形因素及地下水状况的6个代表性特征进行。这些特征包括岩土体重度(γ)、黏聚力(c)、内摩擦角(φ)、坡角(α)、坡高(H)及孔隙水压力比(γw)。通过查询文献、数据汇编(Zhang et al.,2022),本文收集了505组边坡样本,其中 263 组样本处于稳定状态,242 组样本处于破坏状态。由于篇幅限制,在此仅列出了 10 组样本(表2)。
表2边坡稳定性数据集样本(部分)
此外,本研究还收集了研究区域的工程地质、水文地质资料,以及大量滑坡灾害的勘查数据,这些数据的收集有助于全面了解研究区域的特征和背景信息。
2 基于优化算法优化神经网络的边坡稳定性评价模型
将神经网络的方法应用到边坡稳定性评价中,搭建了边坡稳定性评价模型。优化算法的选取影响着边坡稳定性评价结果的好坏,因此对优化算法的选择显得十分必要。
基本思路是:(1)对收集的边坡数据进行预处理,并作为神经网络的学习样本;(2)利用训练集的数据构建不同优化算法的神经网络模型;(3)对模型参数进行调整;(4)使用测试集的数据进行验证; (5)得到表现最好的模型,将其应用于边坡稳定性评价。
2.1 数据预处理
不同参数的量纲和单位不同,数据值往往不在同一量级上,这可能会导致神经网络无法收敛。因此,采用最小—最大比例来将这些变量进行归一化处理,公式如下:
(6)
式(6)中:x 为数据集中的数据,xmin为最小值, xmax为最大值;f(x)是归一化后的数据。
2.2 神经网络参数的确定
岩土体重度、内摩擦角、黏聚力、坡高、坡角及孔隙压力比作为神经网络的 6 个输入参数,稳定性状态为输出值,输出值通过 round函数进行处理,如果输出值为 1代表边坡稳定,为 0则代表边坡破坏。因此,网络的输入单元数是 6,输出单元数是1,隐藏层神经元数可根据式(7)选取,通过试错法分析,本文隐藏层神经元个数选择15。
(7)
式(7)中:Nhid为隐藏层神经元个数;Ninput为输入层神经元个数;n为1~10之间的整数。
理论上,单隐层神经网络可以拟合任意的非线性函数。为了防止在训练出现过拟合,将隐藏层的层数设置为 1,BP 神经网络的最大训练步数设为 10000步,训练误差目标为10-6,选用tansig函数作为隐含层的传递函数,purelin 函数作为输出层的传递函数,采用贝叶斯正则化算法对获得最优初始权重和阈值的BP神经网络进行训练,因此性能函数由误差平方和(ED)和神经网络参数和(EW)组成,如式 (8)所示。贝叶斯正则化算法推导过程的细节步骤参考 MacKay and David(1992)。当神经网络参数在下一次迭代过程中没有发生显著变化时,网络就已经训练成熟。
(8)
式(8)中:E 为性能函数;x 是输入特征的向量; hw(x)是假设函数;α和β为正则化系数,在训练阶段按照贝叶斯规则进行优化;n 为训练数据的个数;qi 是与输入参数相对应的实测偏应力;而 wj是神经网络连接权重。
2.3 预测模型与结果分析
2.3.1 预测模型

图3数据集箱线图
MEA模型训练中的趋同过程如图4、图5所示,进行多次的趋同步骤,各子种群的得分不再发生变化时,就代表这些种群的周围都没有发现更优的个体,即完成初步趋同。对比图4和图5可看出,全部子种群成熟以后,临时子种群中3高于优胜子种群4的得分,因此还需要进行异化操作(滕文龙等, 2021)。
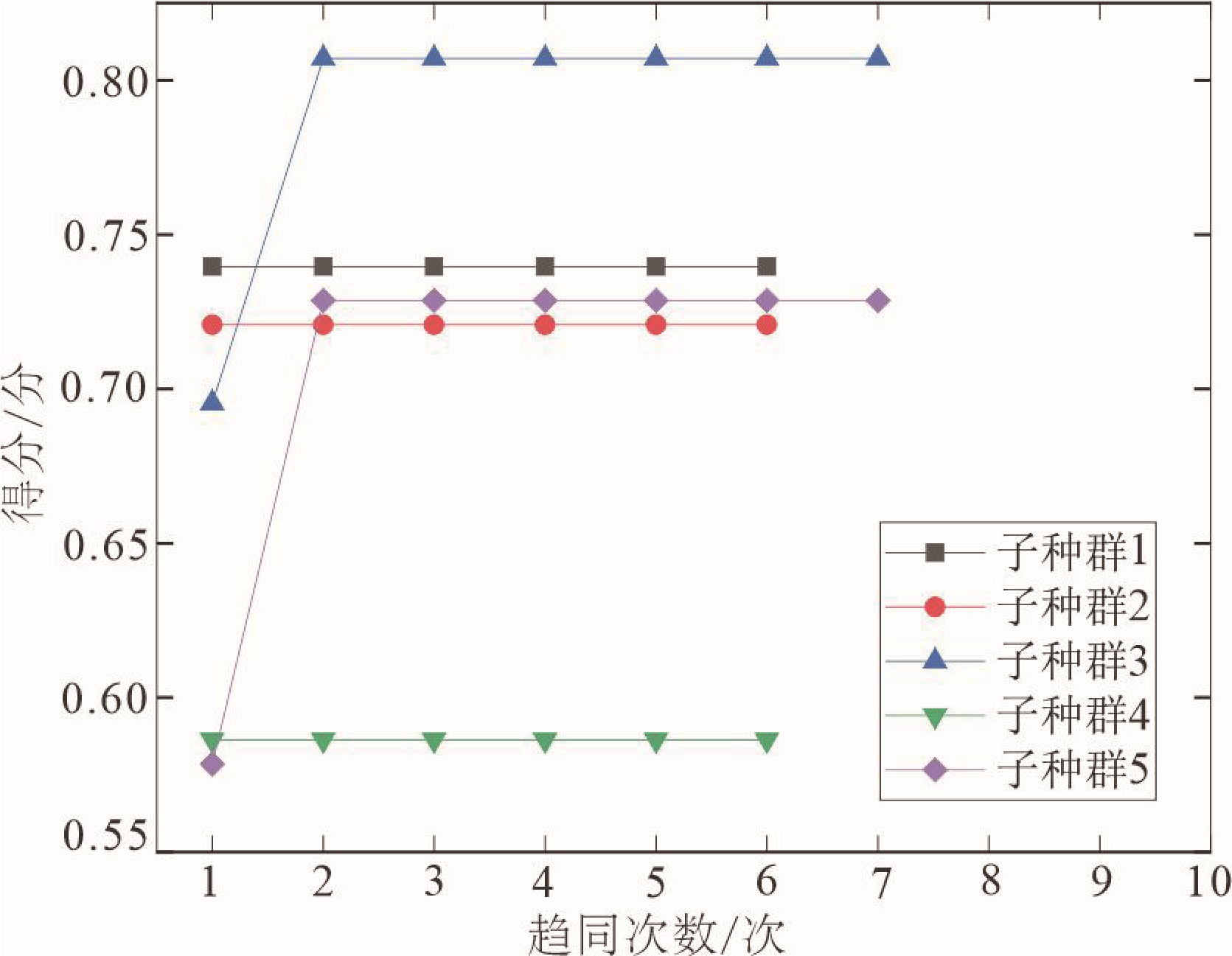
图4临时子种群趋同步骤

图5优胜子种群趋同步骤
经过异化操作后,再进行新的趋同,如图6、图7所示,从图中可以发现临时子种群的得分均低于优胜子种群,趋同和异化步骤就完成了。
2.3.2 不同优化算法的神经网络模型分析
对 MEA-BP、GA-BP、SSA-BP 和 BP 这 4 种网络模型分别进行训练,由图8可以看出,对于同样的数据集,相较于其他的优化算法,MEA-BP神经网络在训练过程中的AUC更高,这表明MEA-BP神经网络的预测结果更加趋近于训练样本的实际情况。
表3数据的统计描述
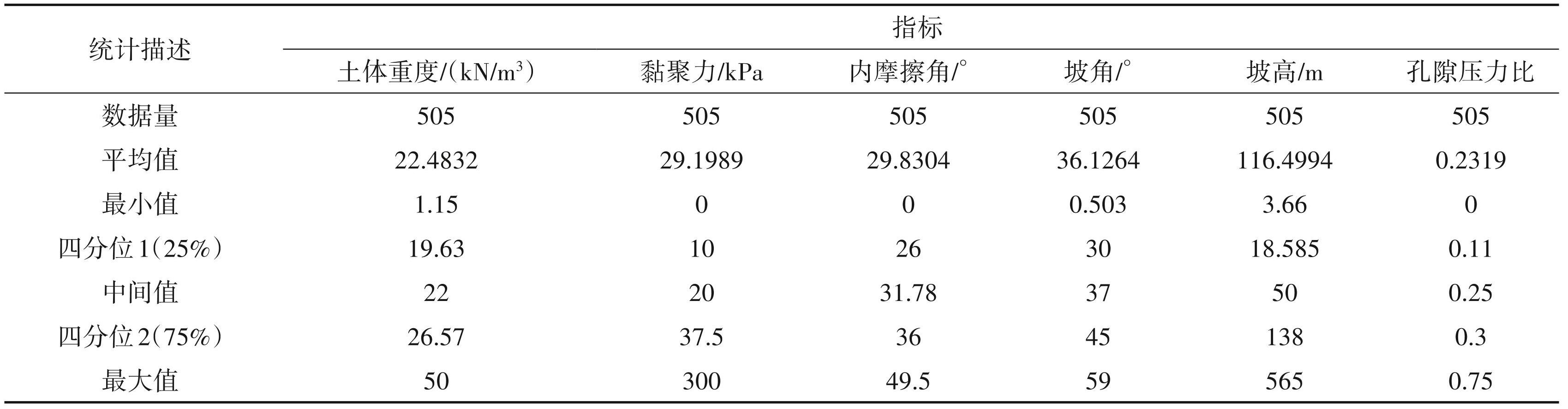

图6异化后的临时子种群趋同步骤

图7异化后的优胜子种群趋同步骤
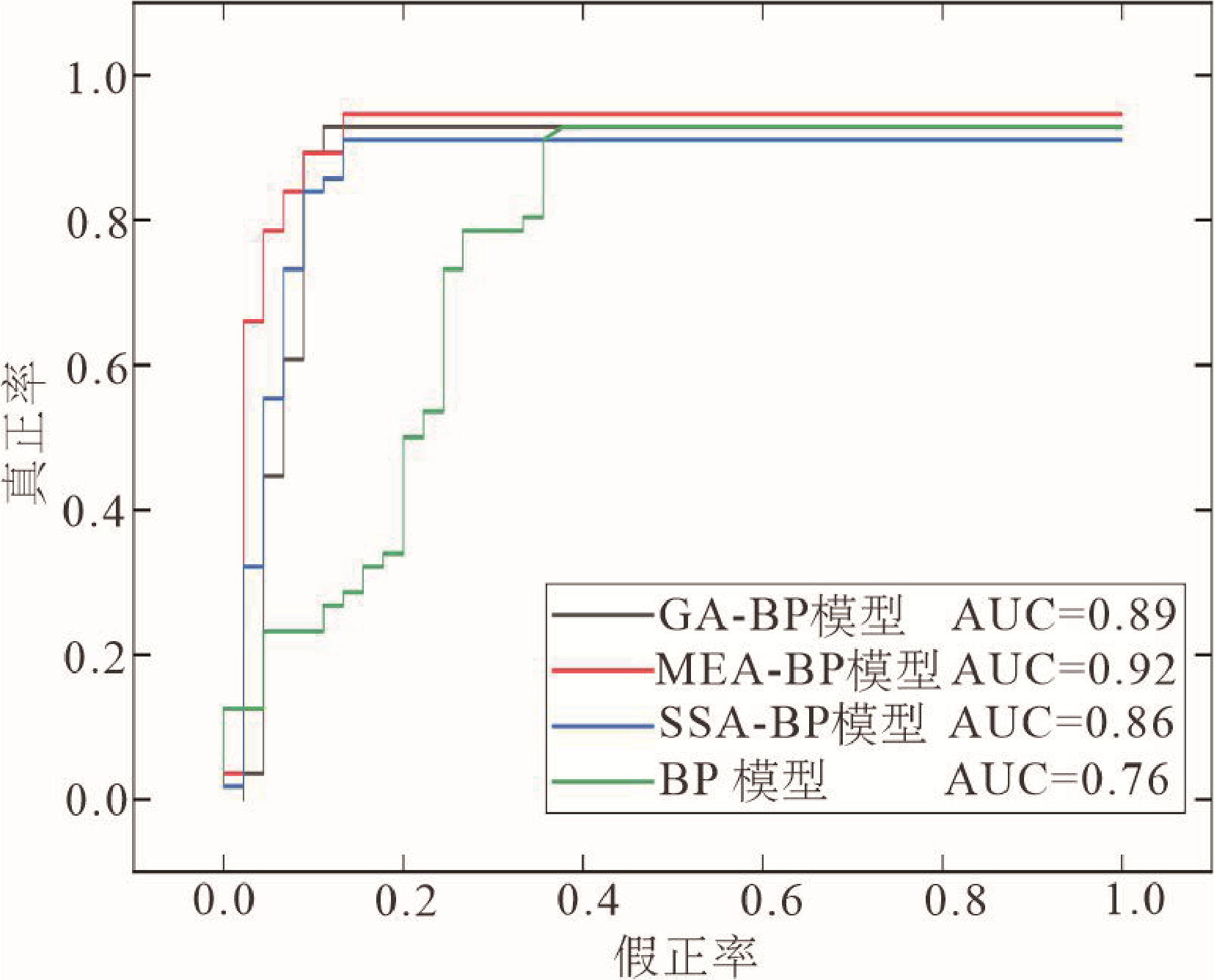
图8ROC曲线图
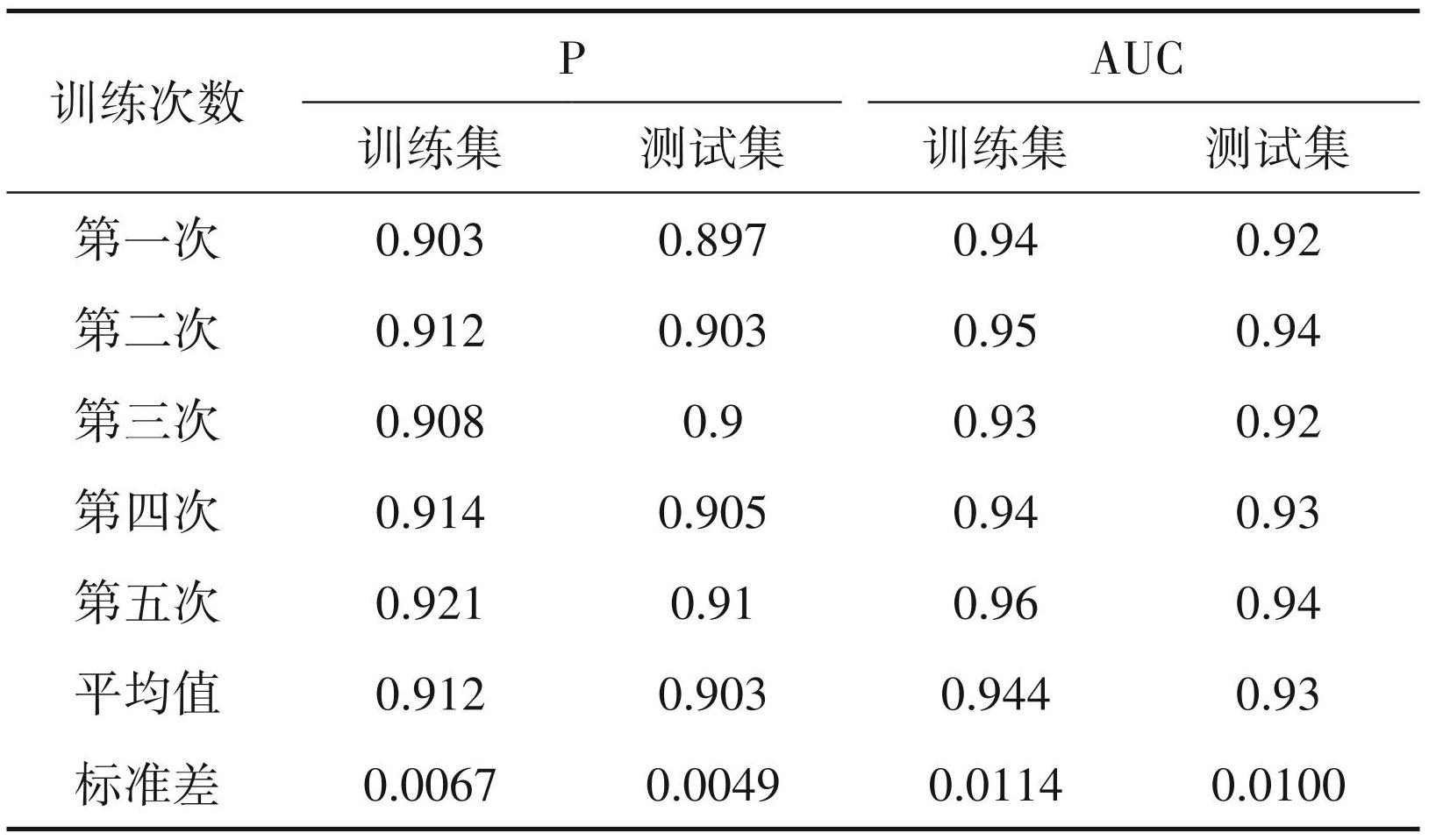
为了得到一个稳定的结果,应用 MEA-BP 神经网络训练的同时,采用五折交叉验证的方法(张新生和蔡宝泉,2021),将数据集随机分成 5 个独立的子集,每个子集有101个数据点,以评估神经网络的性能。每个子集分别被指定为测试集,而其余子集被用于训练神经网络。然后在相应的测试集上对经过训练的神经网络进行评估,以确定其预测性能的稳定性。利用精确率(P)和AUC这两种常用统计测量值,来评估神经网络的性能。表4为 MEA-BP 在训练集和测试集上神经网络性能的统计测量值,从中可以发现 MEA-BP 精确率 P 的平均值为 0.903,且 AUC 的平均值接近 1,表明 MEA-BP 神经网络的预测性能比较稳定,而且能够提供较精确的预测结果。
表4MEA-BP神经网络性能在训练集和测试集上的统计测量值
3 三峡库区边坡实例分析
三峡工程是一项超巨型工程,对国家经济的长远发展和人民的安危祸福有直接影响(中国科学院成都图书馆和中国科学院三峡工程科研领导小组办公室,1987)。三峡工程的成败关键在于移民工作的顺利进行,而为了确保可靠评价高切坡的稳定性,需要全面了解工程库区的工程地质和水文地质条件。同时还需要对已经发生的崩塌和滑坡进行研究,包括其类型、规模、形成条件和稳定性状态等 (长江水利委员会,1997)。因此,准确预测三峡库区边坡稳定性不仅具有学术研究意义,同时也为实际工程提供了参考性。
3.1 实例分析
为进一步分析 MEA-BP 神经网络的泛化性能,将上面训练成熟的网络应用于三峡库区的边坡稳定性预测。首先通过文献及资料收集三峡库区边坡的工程地质以及水文地质条件,具体数据如表5所示。然后用已经训练成熟的网络去预测三峡库区边坡的稳定性,最后与实际的边坡稳定性进行对比分析。
表5三峡库区边坡样本
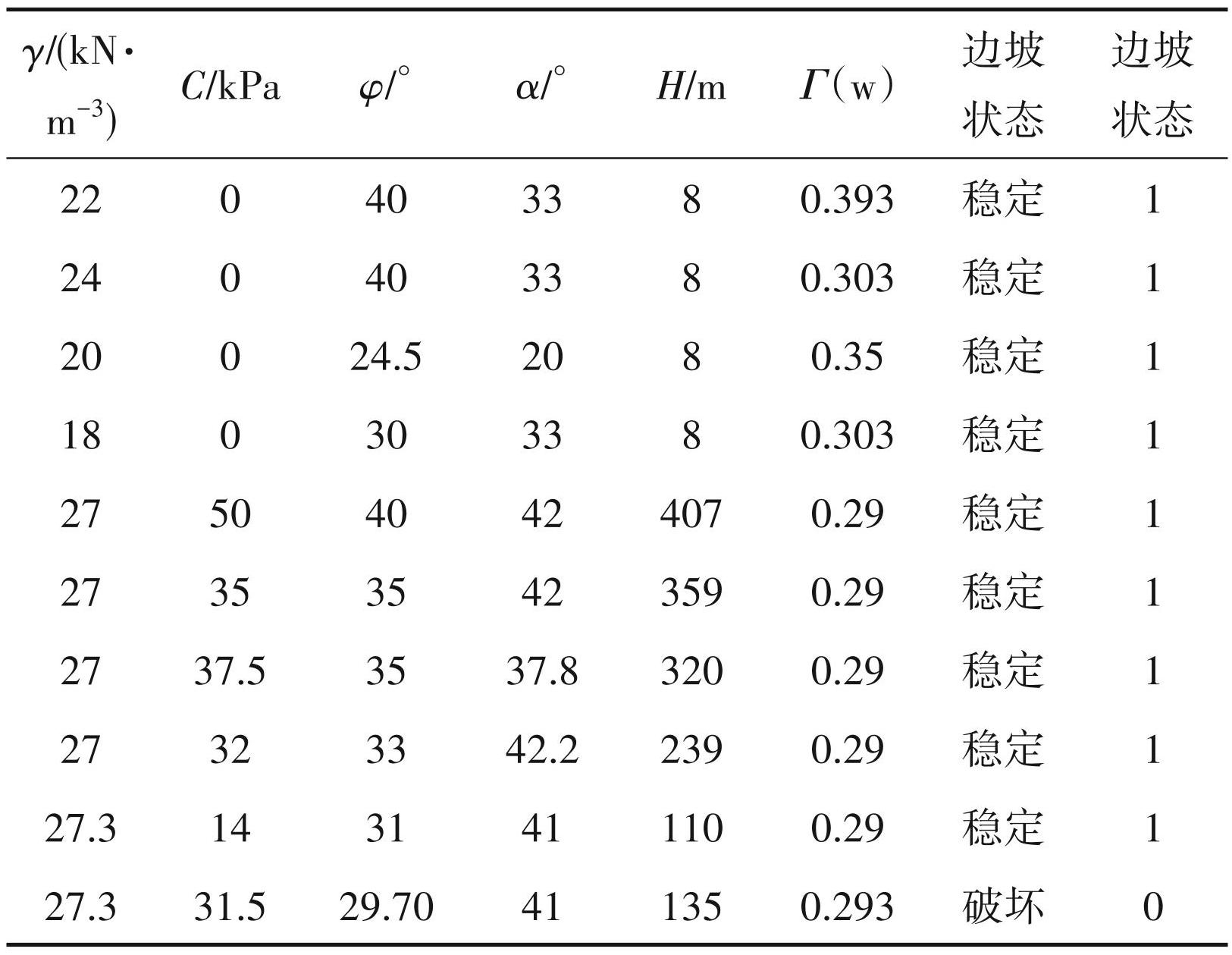
表6三峡库区边坡稳定性对比
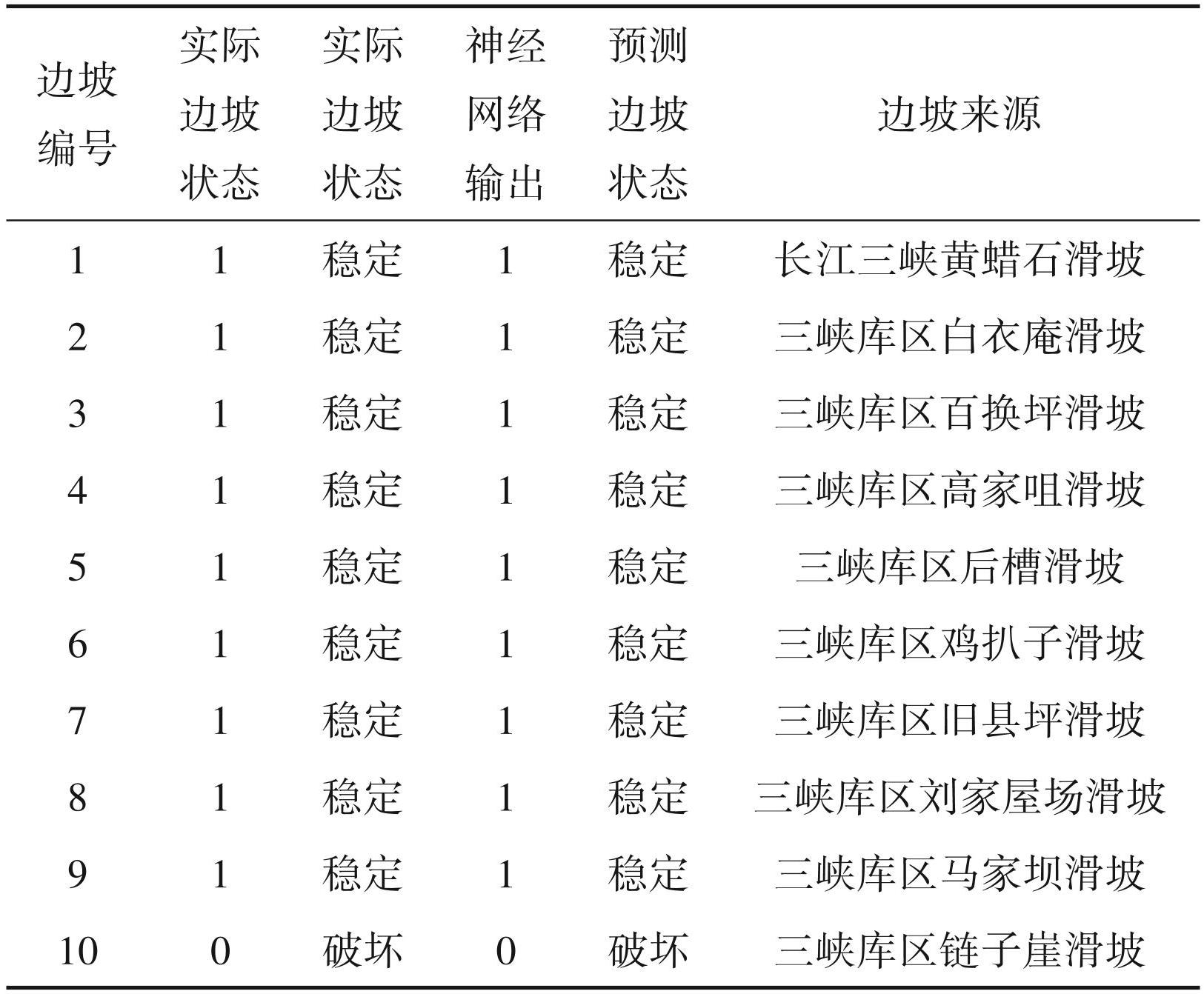

图9三峡边坡稳定性预测ROC曲线图
基于 MEA-BP 预测三峡库区边坡稳定性的结果如表6和图9所示,从中可以发现,MEA-BP 神经网络预测三峡库区边坡稳定性的准确率是 100%,AUC 值为 1,表明了 MEA-BP 在预测边坡稳定性方面的优越性。
3.2 基于神经网络模型的方程
综上所述,所提出的神经网络模型能够准确预测边坡的稳定性。为了在实际问题中得到应用,本文开发了一个基于神经网络的公式。将K值作为输出响应,本文采用了前文给出的程序。通过使用激活函数、权重、偏差和归一化因子,直接从开发的神经网络模型中得到K的显式表达式,表示为:
(9)
式(9)中,KN为滑坡的归一化输出。式(9)的形式来源于式(6)的反归一化过程,因此0.5为数据库输出最大值和最小值差的一半。归一化值 KN为函数,由下式表示:
(10)
(11)
式(11)中:F1,F2,F3,···,F6为归一化处理后的输入值,其可以通过主成分系数矩阵和原始输入参数转化得到,其他系数h0-hn和ci0-ci6见表7。
表7边坡稳定性预测公式的系数

4 结论
本文据 Zhang et al.(2022)边坡数据,从岩土体重度、内摩擦角、黏聚力、坡高、坡角及孔隙压力比共 6 个维度建立边坡稳定性评估体系,通过本文提出的基于思维进化算法优化的 BP 神经网络模型来预测边坡的稳定性,并得到以下结论:
(1)本文对不同优化算法优化的BP神经网络进行了预测性能对比,研究结果表明:相较于其他的优化算法,MEA-BP 神经网络训练过程中的AUC更高,且MEA-BP的泛化能力更强。
(2)基于五折交叉验证和统计结果可以发现, MEA-BP 神经网络的预测性能较为稳定,且可以较精确地预测不同工程地质条件下边坡的稳定性。此外,预测结果与试验实测结果的偏应力分布非常相似。与数值模拟方法相比,本文所提出的方法只需要输入6个参数,可以通过地质资料直接获得,对于参数的要求更低。
(3)通过对三峡库区边坡实例分析,验证了 MEA-BP神经网络模型是适用的。MEA-BP神经网络模型在预测边坡稳定性方面表现出色。基于 MEA-BP 的方法具有结构简单和灵活性强的优点,它可以随着数据量的增加考虑更多影响边坡稳定性的潜在因素。因此,该方法有望成为一种估计边坡稳定性的通用方法。
(4)本文提出了一种基于神经网络模型的计算边坡稳定性的公式,该公式考虑了所有 6 个影响边坡稳定性的成分。此系统可以应用到其他区域的边坡上,为研究人员提供预测数据资料。















