摘要
在带状地物压覆陡倾矿体范围的空间投影变换过程中,因作图与计算方法不正确,常常会造成压覆矿体边界范围和压覆矿产资源储量就会出现偏差,探求能正确圈定压覆矿体水平投影范围和垂直纵投影范围的计算方法,以期达到正确估算压覆重要固体矿产资源储量的目的。按照由简单情形至复杂情形的递进研究思路,分规则带状地物垂直投影基准线、规则带状地物斜交投影基准线、不规则带状地物斜交投影基准线三种情形,基于投影基准线的压矿边界范围水平投影/倾斜投影/垂直纵投影间的三角函数关系,推导其空间投影变换过程中的数学计算公式,为科学圈定压矿边界范围,正确估算压覆资源储量提供数学基础。设带状地物长轴延伸方向长度为L,α为矿体倾角,β为基岩移动角/裂缝角,γ为带状地物长轴延伸方向与投影基线间的交角,在空间投影变换过程中,通过其空间三角函数关系的推导,其结果是:在水平投影图上,安全岩柱沿投影基线方向的宽度W 水平1=L∙sinγtanαcotβ,沿带状地物长轴延伸方向的宽度W 水平2=L ∙sinγtanαsin(90-β)cos(arctan(tanαsinγ))/sin(β-arctan(tanαsinγ));在垂直纵投影图上,安全岩柱沿投影基线方向的宽度(W 垂直1 )与其在水平投影图上的宽度相同(W 水1 ),沿带状地物长轴延伸方向的宽度W 垂直2= L∙sin2γtan2αsin(90-β)cos(arctan(tanαsinγ))/sin(β-arctan(tanαsinγ))。分别在水平投影图和垂直纵投影图上,依次编联安全岩柱拐点,即可得到水平压覆范围和垂直纵投影压覆范围。利用空间投影变换过程中的三角函数关系,通过数学方法求算编联地表不规则带状物压覆陡倾矿体的水平投影和垂直投影的边界范围,为压覆矿产资源评估提供了正确的计算作图思路与具体方法,方便地质技术人员在计算作图直接引用,具有很强的实践意义。避免地质技术人员在实际作图过程中,因错误地理解空间投影变换和繁琐的计算公式推导,常常导致的压矿边界范围错误编联和压覆资源储量估算结果出现偏差问题。利用本文研究结果,可进行空间投影变换三维可视化计算成图软件开发,提高作图效率和准确度,起到事半功倍的作用。
Abstract
Due to incorrect mapping and calculation methods, the boundary range of the ore body and the reserves of the mineral resources are often deviated during the transformation of the space projection of the area of the steeply-sloping ore body in the zonal ground features. A calculation method that can correctly delineate the horizontal projection range and vertical longitudinal projection range of the ore body is sought to achieve the purpose of correctly estimating the reserves of the important mineral resources. According to the progressive research idea from simple case to complex case, three cases are divided into vertical projection datum line of regular strip surface objects, oblique projection datum line of regular strip surface objects and oblique projection datum line of irregular strip surface objects. Based on the projection datum line, the trigonometric function relationship between horizontal projection, oblique projection and vertical longitudinal projection of ore mining boundary range is obtained. The mathematical calculation formula in the process of space projection transformation is derived, which provides mathematical basis for scientifically delineating the boundary range of compressed ore and correctly estimating the reserves of compressed resources. The length of the long axis extension direction of the zonal surface object is L,α is the dip Angle of the ore body,β is the bedrock movement Angle/crack Angle, and γ is the intersection Angle between the extension direction of the zonal surface object's long axis and the projection base line. In the process of spatial projection transformation, through the derivation of its spatial trigonometric function relationship, the results are as follows: On the horizontal projection diagram, the width of the safety pillar along the projection base direction Whorizontal1=L ∙ sinγtanα coβ, The Whorizontal2=L ∙ sinγtanαsin(90- β) cos (arctan (tanαsinγ)) /sin(β-arctan (tanαsinγ)) along the long axis of the strip; On the vertical vertical projection chart, the width of the safety pillar along the projection base direction (Wvertical1 ) is the same as that on the horizontal projection chart (Whorizontal1 ). Width Wvertical2=L ∙ sin2γtan2αsin(90- β) cos (arctan(tanαsinγ)) /sin(β -arctan (tanαsinγ)) along the long axis of the strip. The inflection points of the safety pillar can be sequentially linked on the horizontal projection diagram and the vertical longitudinal projection diagram respectively, and the horizontal and vertical longitudinal projection can be obtained. By using the triangular function relation in the process of spatial projection transformation, the plane projection range and vertical projection range of the irregular belt on the surface of the surface are realized by mathematical method, which provides a correct mapping idea and a reliable mapping method for the assessment of the resource and reserves. In the process of actual mapping, the geological technicians will avoid the wrong delineation of the overburden area and the wrong evaluation result of resource reserves due to the wrong understanding of the spatial projection transformation. In the future work process, the development of three dimensional visual display and spatial projection transformation program can be further carried out to save the cumbersome calculation process and improve the efficiency and accuracy of mapping.
0 引言
建设项目压覆重要矿产资源评估工作是一项重要工作。既能避免或减少压覆重要矿产资源,保护矿产资源,提高矿产资源保障能力,又可保障建设项目正常顺利进行。同时,还对维护矿业权人合法权益,妥善解决建设单位与矿业权人间的纠纷发挥重要作用。按照《自然资源部关于深化矿产资源管理改革若干事项的意见 》(自然资办发〔2023〕6 号),建设项目压覆重要矿产属于五种需要编制矿产资源储量报告,并需要申请评审备案的情形之一 (①探矿权转采矿权、②采矿权变更矿种或范围、③ 油气矿产在探采期间探明地质储量、④其他矿产在采矿期间累计查明矿产资源量发生重大变化(变化量超过 30% 或达到中型规模以上的)、⑤建设项目压覆重要矿产),可见建设项目压覆重要矿产资源评估与审批管理工作的重要性。压覆重要矿产资源储量估算是编制建设项目压覆重要矿产资源评估报告中的核心内容,定量阐述压覆矿产资源储量的平面范围、空间分布、质量、数量及其经济意义。正确估算压覆重要矿产资源储量是反映报告质量的重要指标之一,对于建设项目压覆重要矿产资源评估工作显得至关重要。众多矿产资源储量专家在此方面开展过诸多卓有成效的研究(李再兴等, 2014;赵建平,2014;王才川和周晓萌,2017;黄继超等,2018;李光明和褚敬,2019;刘流等,2020;韩政兴等,2021;刘玥等,2021;马伟亮,2022;孙秀菲, 2022;张闯和王苒,2022;周鼎等,2022;刘杰等, 2023;曲俊利等,2023;向钊等,2023;于沙沙,2023a,2023b;陈敏等,2024)。
通常情况下,压覆重要矿产资源储量估算是在最近报告的基础上,利用原报告中的资源量估算图,按照相关规程、规范要求,进行压覆范围的确定和资源储量的块段分割计算与统计汇总。固体矿产资源量估算方法有几何法、地质统计学法、距离幂次反比法和布局曲线积分储量计算及动态分维储量审定法(SD法)等,其中几何法中的地质块段法是最常用的一种,通常适用于二维延展矿体。地质块段法资源量估算图常用的有两种投影方式,当矿体倾角较缓时,采用水平投影;当矿体倾角较陡时,采用垂直纵投影。对于水平投影资源量估算图而言,无需空间投影变换,直接在水平投影图上进行压覆范围的圈定和压覆资源储量块段分割计算;对于垂直纵投影资源量估算图而言,就需要通过正确的空间投影变换,方能正确圈定压覆矿体的水平投影范围和垂直纵投影范围,并在垂直纵投影资源量估算图上估算压覆量,显然较水平投影资源量估算图的作图过程复杂一些。
工作实践过程中,经常会遇到因空间投影变换方法不正确,多造成压覆边界范围在水平投影图和垂直纵投影图上的圈联不正确,平面投影/倾斜投影/垂直纵投影压覆范围和位置互不对应,更重要的是压覆资源储量块段分割与计算结果也会出现偏差,从而影响压覆报告质量。特别是评估对象为不规则带状物,如水电站河流库区、交通道路及输送管廊等,如空间变换及计算作图不正确,压覆范围和压覆量就会出现更大偏差。目前,尚无一套可利用的空间投影变换的数学方法、计算公式和作图步骤,因此,有必要基于垂直纵投影资源量估算图,以不规则带状物压覆陡倾斜矿体为例,探讨其空间投影变换过程中计算与作图,以期获取正确的压覆固体矿产的范围和压覆量,防止评估对象保护范围的错误圈定和压覆资源储量错误估算,为压覆审批管理和压覆固体矿产资源评估提供可靠依据。
以倾斜投影为纽带,在倾斜投影图上分别圈定压覆评估范围和留设安全岩柱范围,二者合并为压覆矿体范围(或称为压覆固体矿产资源范围)。在此基础上,通过空间投影变换,将倾斜投影压覆范围转换为水平投影压覆范围,以明确地表地物的地面压覆与保护的边界范围;继而将倾斜投影压覆范围转换为垂直纵投影压覆范围,为压覆矿体资源储量分割计算与统计汇总提供依据。为方便讨论,将带状地物、矿体水平投影图、倾斜投影图及垂直投影图简化为模型,放在立体几何图中便于研究其三角函数关系,并按照由简至繁的递进研究思路,分情形、分步进行讨论。
1 规则带状物长轴垂直于投影基准线(矿体走向)情形一
1.1 压覆矿体范围在水平投影图上的圈定
如图1所示,设 OPMN 表示规则地面带状建 (构)物受护边界范围或水体最高洪水线范围(水电站库区为千年校核洪水位),L代表带状建(构)物长轴延伸方向长度,即 L=PM。ABEF表示矿体倾斜投影面,ABCD 表示矿体水平投影面,ABGH 表示矿体的垂直纵投影面。AB表示矿体的投影基线,即矿体走向线,也代表矿体露头线。本文列举地面带状物长轴方向垂直于矿体走向情形,即 PM⊥AB。 OPM'N'表示地面带状物受护范围的倾斜投影压覆评估范围,OPM″N″表示地面带状物受护范围的垂直纵投影压覆评估范围。OPXY表示地面带状物水平投影压覆范围,OPX'Y'表示地面带状物倾斜投影压覆范围,OPX″Y″表示地面带状物垂直投影压覆范围。
假设矿体倾角为α(α≥60°)。为方便讨论,假定地表及其以下均为基岩,也暂且不考虑采深采厚比,基岩移动角(水体压覆为裂缝角)设定为 β,且 α <β。只需分别计算作图带状物O、P、M、N这4个拐点对应的压覆矿体点的水平投影点,并依次编联,即可得到地面带状物压覆矿体的平面范围(OPXY)。
由于受护边界拐点 O、P 点位于矿体露头线 (AB)上,矿体直接暴露地表,容易理解 O、P 点也同压覆矿体点,关键在于求算受护边界拐点M、N沿走向和倾向的安全岩柱宽度(W 水平1、W 水平2)。假设 M 点在倾斜投影面(ABEF)的铅直投影点为 M';考虑移动角情形下,M点沿投影基线AB(矿体走向)在倾斜投影面(ABEF)安全岩柱边界点为 I'。如图2所示,计算方法如下:
因为MM'=PM∙tan α,且M'I'=MM'∙cot β
所以M'I'= PM∙tan α cot β。
I'点位确定后,根据其空间几何关系,容易得知 MI=M'I',即在水平投影面上,沿投影基线方向安全岩柱宽度(W 水平1)=MI=PM∙tan α cot β,即 W 水平1=L∙ tan α cot β。沿 M平行投影基线 AB(矿体走向)做线段 MI,得到 M 点沿走向的安全岩柱边界水平投影点(I)。
PM⊥AB得知,地物受护拐点M在水平投影面上沿长轴延伸方向,就是在倾斜投影面(ABEF)沿倾斜延深。考虑移动角情形下,设其在倾斜投影面上的压覆点为 S',如图3所示,在△MM'S 中,已知 MM', ∠M'MS'=90-β,∠MM'S'=90+α,∠M'S'M=β-α。其计算公式推导如下:
过 M' 点做 △ MM'S 中的垂高线,设垂高为 h。则:
因为h/ MM '=sin(90-β),h= MM '∙sin(90-β)
所以h/M'S'=sin(β-α),M'S'= h/sin(β-α)。
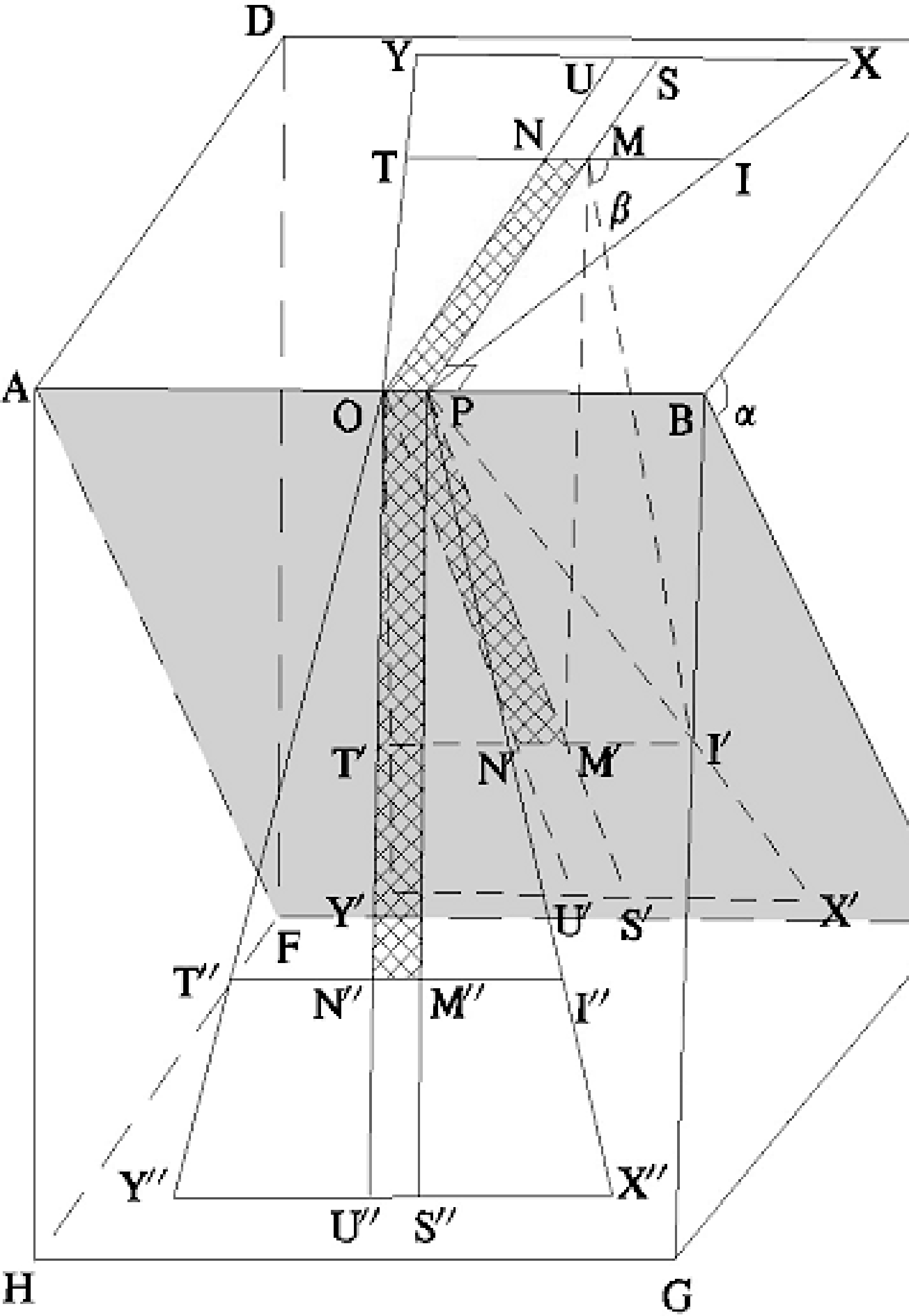
图1压覆矿体水平投影/倾斜投影/垂直纵投影立体透视图
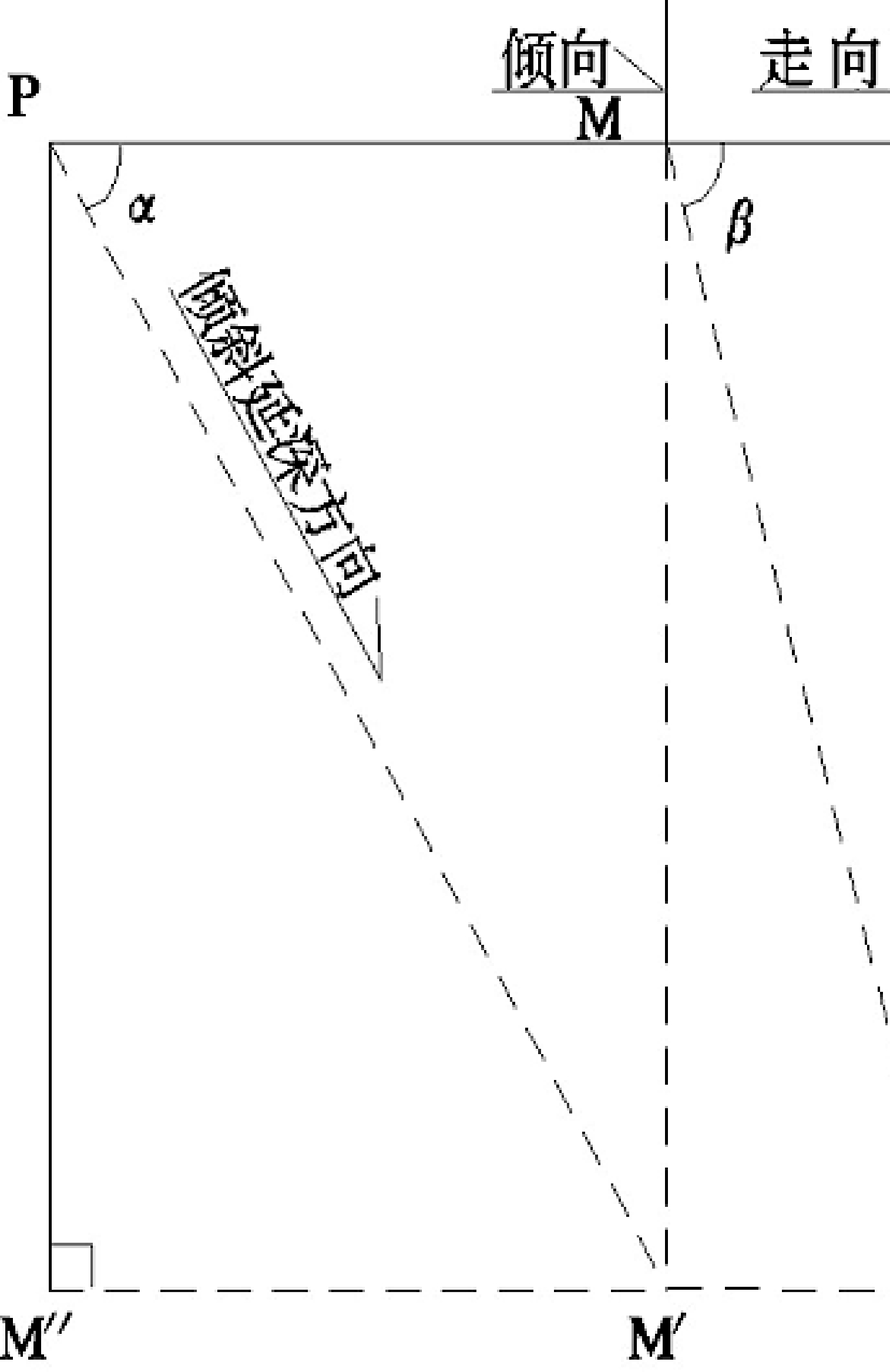
图2压覆矿体倾斜剖面(左)与走向剖面(右)图
由上式可得M点在ABEF面上沿倾斜延深方向上的安全岩柱边界点S'。
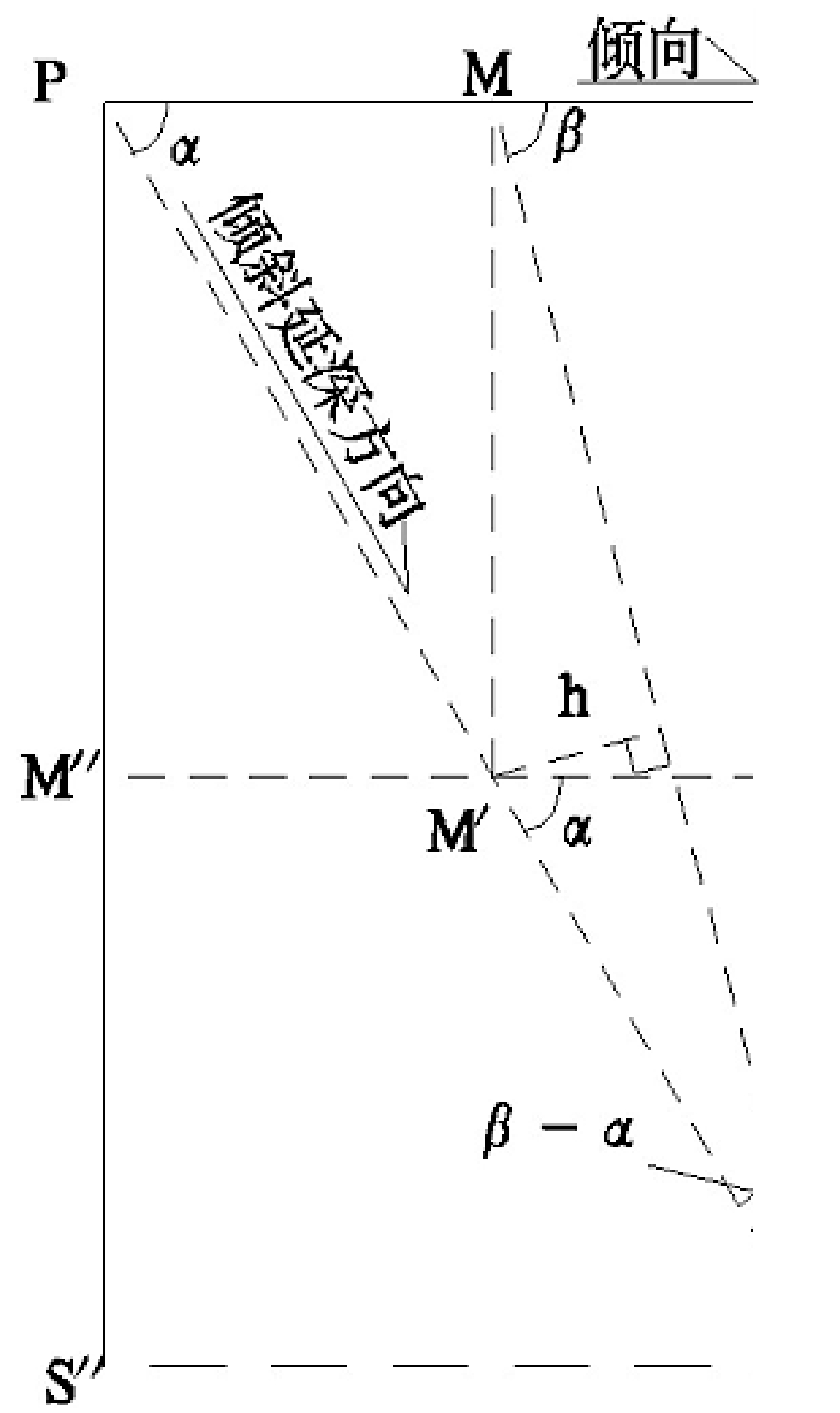
图3压覆矿体倾斜剖面图
将 S'点向上铅直投影到水平面上,得安全岩柱边界点S'点的水平投影S点,MS代表在水平投影面上 M 点沿倾斜方向安全岩柱宽度(W 水平2)。计算公式推导如下:
因为M'S'= MM'∙sin(90-β) / sin(β-α),且MS= M'S'∙cosα
所以MS= MM'∙cosαsin(90-β) / sin(β-α)
又因为MM'=PM∙tan α
所以 MS=PM ∙ sinαsin(90-β) / sin(β-α),即 W 水平2=L∙sinαsin(90-β) / sin(β-α)。
按照上述作图投影思路,同理得到边界拐点 N 沿投影基线 AB 在倾斜投影面上的安全岩柱边界点 (T')及其在水平投影图上的安全岩柱边界点(T),N 点沿矿体倾斜延深方向的安全岩柱边界点(U')及其水平投影图上的安全岩柱边界点(U)。过S、U点做直线,分别于 PI 和 OT 延伸线相交于 X、Y 点,在 ABCD 水平投影面上,依次编联 O-P-X-Y-O 点,即可得到压覆矿体水平投影范围(图1),在ABEF倾斜投影面上,依次编联 O-P-X'-Y'-O 点,即得到在矿体在倾斜投影压覆范围。
1.2 压覆矿体范围在垂直纵投影图上的圈定
将倾斜投影面(ABEF)上的 X'、Y'点,通过垂直投影变换,在垂直投影图上(ABGH)得到对应的 X″、 Y″投影点,依次编联 O-P-X″-Y″-O 点,即得到地面带状物的垂直纵投影压覆矿体范围。具体可利用其三角函数关系,推导计算公式,按照其计算结果进行作图,编联在垂直纵投影图上的压覆矿体范围。在垂直纵投影图上,设 M″为 M'的垂直纵投影点,I″为 M″点沿投影基线方向的安全岩柱边界点, M″I″即为安全岩柱沿投影基线方向的宽度(W 垂直1 )。如图2所示,计算公式推导如下:
PM″= MM'=PM∙tan α
在垂直纵投影图上,由上式可得 M″位置。易知:M″I″=M'I'= MI,由M'I'= PM∙tan α cot β可得:
M″I″= PM∙tan α cot β,即 W 垂直1= L∙tan α cot β, W 垂直1=W 水平1。
在垂直纵投影图上,由 PM″= MM'=PM∙tan α, M″I″= PM∙tan α cot β 即可得 I″位置。
沿矿体倾向在垂直纵投影图上安全岩柱宽度 (W 垂直2 )即为M″S″,S″为倾斜投影压覆点S'在垂直纵投影图上的安全岩柱边界点。如图3所示,PS″计算公式推导如下:
PS″=SS'=PS∙tan α
因为 MS=PM∙sinαsin(90-β) / sin(β-α),且 PS= PM+MS
所以PS= PM+PM∙sinαsin(90-β) / sin(β-α)
所以 PS″=(PM+ PM∙sinαsin(90-β) / sin(β-α)) ∙tan α
所以 PS″ = PM∙ tan α(1+ sinαsin(90-β) / sin (β-α))。
在垂直纵投影图上,由上式可得 S″位置。沿矿体倾向在垂直纵投影图上安全岩柱宽度 W 垂直2= M″S″,而M″S″=PS″-PM″,由上可知:
W 垂直2=L∙ tan α sinαsin(90-β) / sin(β-α)。
同理,可以得到边界拐点 N 在垂直纵投影图 ABGH 上,沿投影基线方向(矿体走向)的压覆拐点 T″和沿倾斜延深方向投影点 U″。过 S″、U″点做直线,分别于 P I″和 O T″延伸线相交于 X″、Y″,依次编联 O-P-X″-Y″-O,即可圈定压覆矿体的垂直纵投影范围。
在垂直纵投影资源量估算图,以OPX″Y″为压覆资源量估算边界,对涉及压覆的原地质块段进行分割计算和统计汇总,即可得出压覆矿体资源储量。
2 规则带状物长轴斜交投影基准线(矿体走向)情形二
与前述的第一种情形的区别在于,地表带状物长轴延伸方向与矿体走向(投影基线)呈斜交关系,而非直交关系。空间投影变换和作图的思路是,以矿体倾斜投影图为纽带,对带状物受护边界 (OPMN)压覆进行倾斜投影变换(O'P'M'N'),继而对倾斜投影(O'P'M'N')进行垂直纵投影变换 (O″P″M″N″);在此基础上,综合考虑矿体上覆岩层移动角因素,在倾斜投影图上分别求得地表带状物 O、P、M、N 这 4 个边界拐点在矿体倾斜投影面上的安全岩柱边界点,并对矿体倾斜投影图上的压覆点分别进行水平投影变换和垂直纵投影变换,编联安全岩柱边界拐点,即得到压覆矿体的水平投影范围和垂直投影边界范围(图4),最终在垂直投影资源量估算图上进行压覆量的估算。
2.1 压覆矿体范围在水平投影图上的圈定
如图4所示,设矿体倾角为 α(α≥60°),基岩移动角(库区水体压覆为裂缝角)设定为β,且α<β,带状物与矿体走向线交角位 γ(0°<γ<90°),沿带状物长轴延伸线的倾斜投影线处形成的矿体视倾角为 α'。第一步,求得地物受护边界范围在倾斜投影图上的投影范围与空间位置。
在△PMM'中,∠MPM'=α',依据倾角与视倾角之间的三角函数关系(图5),tanα'=h/b,tanα=h/a, sinγ=a/b,得知:
tanα' = tanαsinγ,即 α' =arctan(tanαsinγ);PM/ PM'=cosα';PM'= PM/cos(arctan(tanαsinγ))。
在倾斜投影面上,求得 α'和 PM',即可确定 M' 在倾斜投影面上的位置。同理,可得N'在倾斜投影面上的位置。上述地物受护边界在倾斜面上的投影,还可用另一种计算方法求得,即分别求得 M 沿投影基线的水平偏移距 PM1 和沿倾斜延深距离 M1M',也可得M'在倾斜面上的位置。计算公式推动如下:
△ PMM1 中,由 PM1/PM=cosγ,得:PM1= PM ∙ cosγ
或者M1位置还通过作图的方法直接获取,即由 M 点向投影基线 AB 做垂线,其垂足位置即为 M1 位置。
△M1MM'中,由 M1 M/M1M'=cosα,得:M1 M'=M1 M/cosα;△PMM1 中,M1M/PM=sinγ,得:M1 M=PM∙sinγ。把 M1M=PM∙sinγ 代入 M1 M'=M1 M/cosα,得: M1M'=PM∙sinγ/cosα。同理,可得 N'在倾斜投影面上的位置。依次编联 O-P-M'-N'-O 边界拐点,即可得到地物受护边界在倾斜面上的投影。

图4压覆矿体水平投影/倾斜投影/垂直纵投影立体透视图
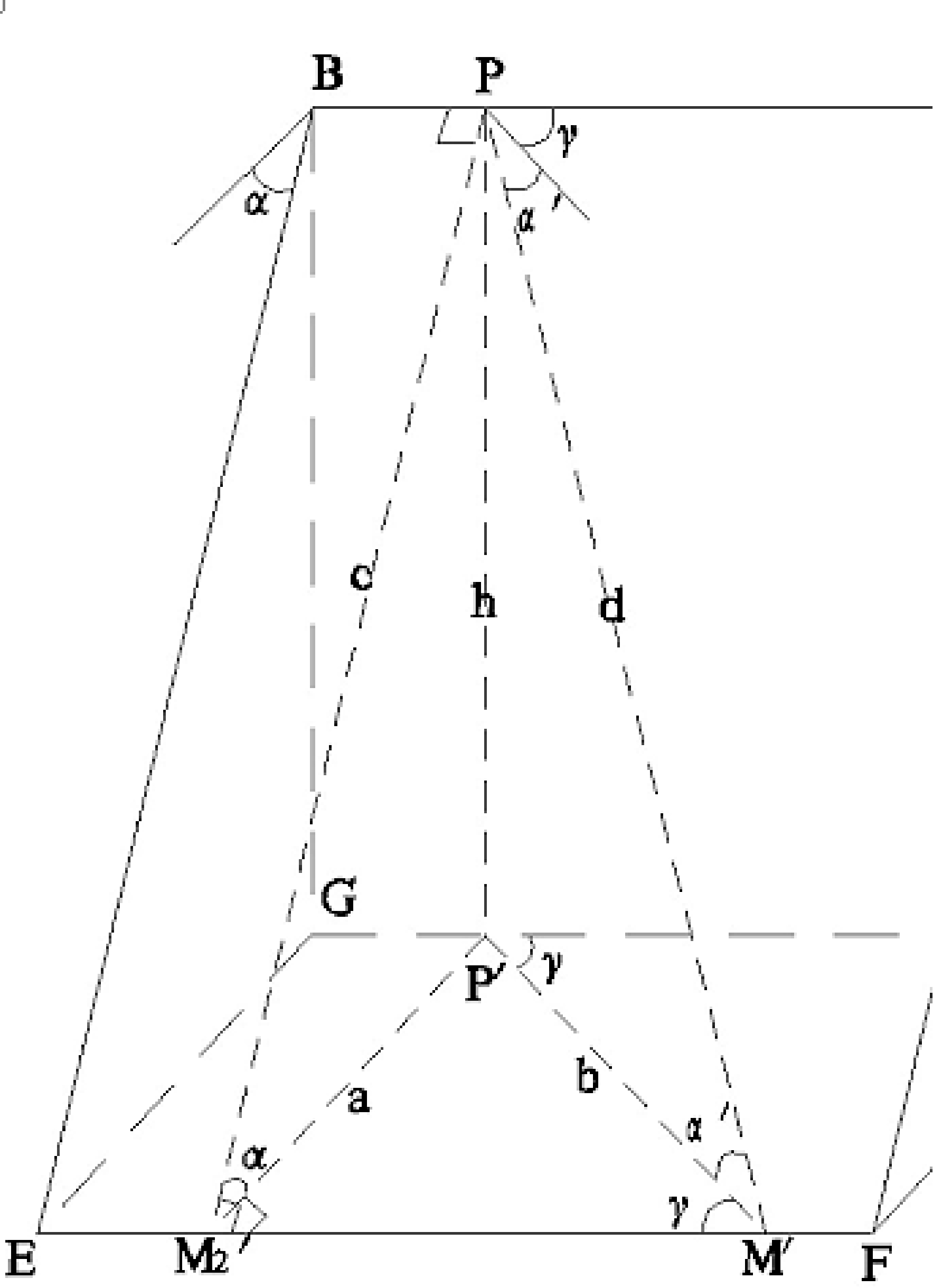
图5真倾角与视倾角关系图
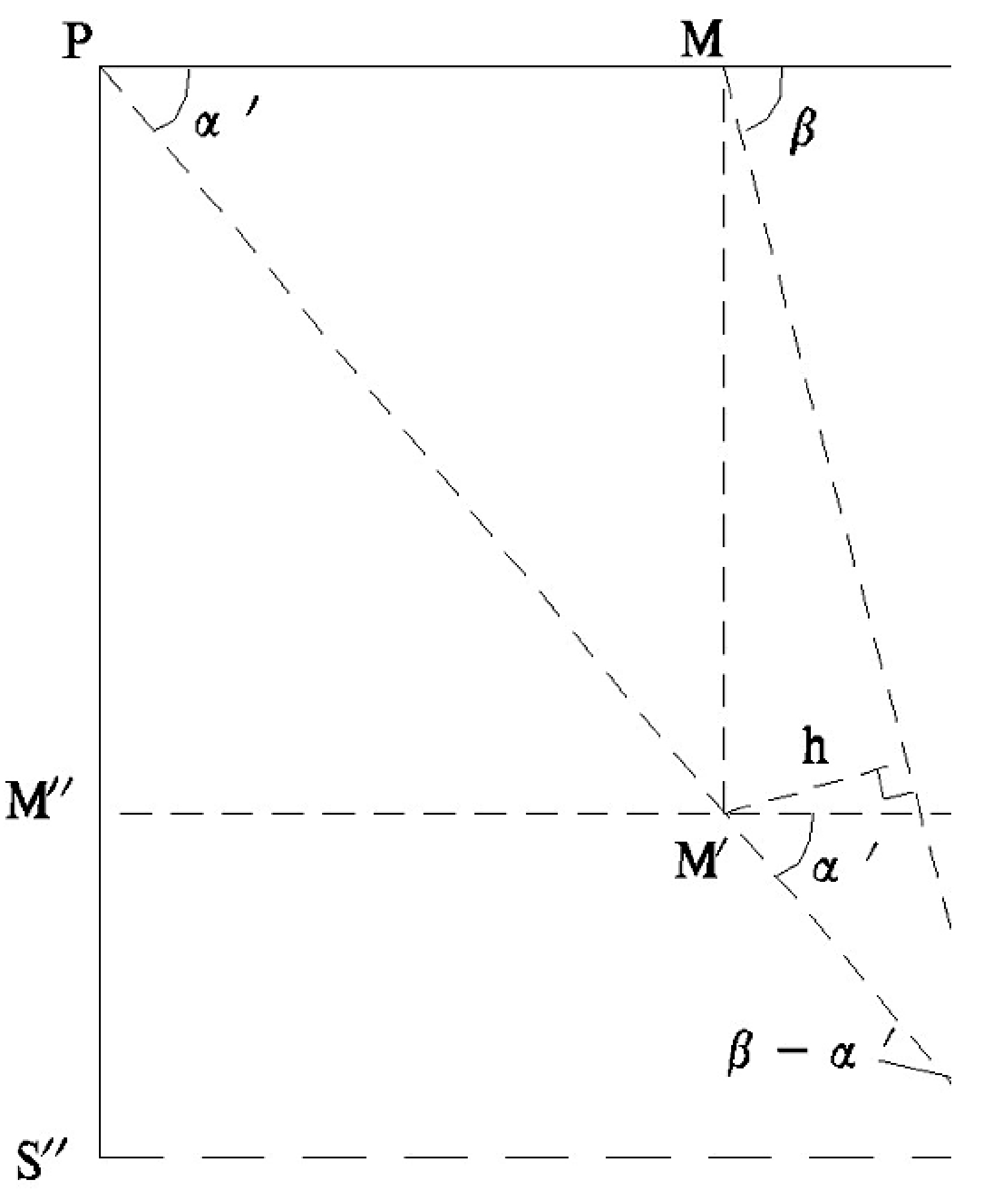
图6压覆矿体倾斜剖面图
第二步,求得安全岩柱边界范围在矿体倾斜投影和水平投影的范围。
设 M 点沿投影基线方向的水平投影压覆点为 I,倾斜投影压覆点 I',求得安全岩柱宽度 MI、M'I',即可得I、I'的水平投影位置和倾斜投影位置。计算公式推导如下:
因为 MM' =M2M2' = PM2 ∙ tanα,eg 且 PM2=PM∙ sinγ,所以MI=M'I'=MM'cotβ
把 PM2=PM∙sinγ代入 MM'=M2M2'= PM2∙tanα,将所得公式带入 MI=M'I'=MM'cotβ,得:MI= M'I'= PM∙sinγtanαcotβ,亦即沿投影基线方向的安全岩柱宽度W 水平1=L∙sinγtanαcotβ。
同理,可到N点沿投影基线方向,在矿体水平投影图上安全岩柱边界点T和在倾斜投影图上的安全岩柱边界点T'。
设M点在倾斜投影面ABEF沿视倾斜延深方向 (带状地物长轴延伸方向)的安全岩柱边界点为 S',在水平投影面ABCD安全岩柱边界点为S,求得MS、 M'S',即可得 S、S'的作图位置。如图6,计算公式推导如下:按照前述投影变换方法可知:M'S'= MM'∙ sin(90-β)/sin(β-α'),由 MM'=M2M2'= PM2 ∙tanα、 PM2=PM ∙ sinγ 式得知,MM' = PM2 ∙ tanα = PM ∙ sinγtanα。把 MM' =PM∙ tan α 代入 M'S' = MM' ∙ sin(90-β)/sin(β-α'),得:M'S'= PM∙sinγtanαsin(90-β)/sin(β-α')
依据倾角与视倾角之间的关系,得知: tanα'= tanαsinγ,即 α' =arctan(tanα ×sinγ)。把 tanα' = tanαsinγ,即 α'=arctan(tanα×sinγ)代入 M'S'= PM∙ sinγtanαsin(90-β)/sin(β-α'),得:M'S' = PM× sinγtanαsin(90-β)/sin(β-arctan(tanα×sinγ)),MS= M'S'∙cosα'。
把 tanα' = tanαsinγ,即 α' =arctan(tanαsinγ)、 M'S' = PM×sinγtanαsin (90-β)/sin (β-arctan (tanαsinγ))代入 MS= M'S' ∙ cosα',得: MS= PM∙ sinγtanαsin(90-β) cos(arctan(tanαsinγ))/sin(β-arctan(tanαsinγ)),亦即沿地物长轴延伸方向的安全岩柱宽度 W 水平2= L ∙ sinγtanαsin(90-β) cos(arctan (tanαsinγ))/sin(β-arctan(tanαsinγ))。
按照上述作图投影思路和方法,同理,可得N点沿矿体视倾斜延深方向的安全岩柱边界点(U')及其水平投影点(U)。过 S、U 点做直线,分别于 PI 和 OT 延伸线相交于 X、Y 点,在 ABCD 水平投影面上,依次编联 O-P-X-Y-O 水平投影压覆拐点,即可得到压覆矿体水平投影范围(图4),在ABEF面上依次编联 O-P-X'-Y'-O 即得到在矿体倾斜投影面上的倾斜压覆范围。
2.2 压覆矿体边界范围在垂直纵投影图的圈定
将倾斜投影压覆点 X'、Y',通过垂直投影变换,得到 X″、Y″,编联 O-P-X″-Y″-O,即得到垂直纵投影压覆范围(图5)。利用三角函数关系进行空间投影变换,计算公式推导如下:
第一步,地表带状物受护边界范围的垂直投影变换。
如图4所示,容易理解 O、P 地物受护边界拐点的压覆点,在倾斜投影图和垂直纵投影图没有位移,均处于原位。以 O、P点为垂直纵投影图上的投影基点,分别求得 M'、N'基于投影基点的水平偏移距(PM1、ON1)和垂距(M1 M″、N1 N″),即可得到 M'、 N'在垂直纵投影图上的位置。计算公式推动如下:
在水平投影图上,过 P 点垂直于投影基线做辅助线,与 MI 的延长线相交于 M2点,并设 M2'点为 M2 点的倾斜投影点。
水平距:PM1=PM∙cosγ。由 tanα= M2 M2'/PM2,sinγ= PM2/ PM,得: M2 M2'= PM ∙sinγtanα。由M1M″ = MM'=M2M2 ',可得垂距:M1M″= PM ∙sinγtanα。
由上述 PM1=PM∙cosγ 和 M1M″= PM∙ sinγtanα 得出:在垂直纵投影图上,M″相对于 P点,沿投影基线走向的偏移距和垂直投影基线的距离,即可得到 M点的垂直纵投影变换点M″的位置。同理,可得N' 在垂直纵投影图上的位置 N″,连接 O-P-M″-N″-O,即可得到地表地物在垂直纵投影图上的投影范围。
第二步,地表带状物安全岩柱范围的垂直纵投影变换。
设 I为 M 沿投影基线方向安全岩柱边界拐点 I' 的水平投影点,S 为 M 沿视倾斜延深方向安全岩柱边界点S'的水平投影点,I″为I'点在垂直纵投影图上沿投影基线的安全岩柱边界变换点,S″为 S'点在垂直纵投影图上沿视倾斜延深方向上的安全岩柱边界变换点。容易得知 M″I″=MI,亦即 W 垂直1=W 水平1。在水平投影图上,过I点垂直于投影基线AB做辅助线,与 AB 相交于 I1点。分别求得 PI1和 I1 I″,即可求得安全岩柱边界点的垂直纵投影位置点(I″);求得 M″S″,沿 P M″延伸方向延长 M″S″,得到安全岩柱边界点的垂直投影位置(S″)。
由图4可知,PI1=PM1-M1I1,M1I1= MI= M'I',M'I' = M M'∙cotβ,由MM'=M2M2'= PM2∙tanα 和PM2=PM∙ sinγ,得:MM' = PM ∙ sinγtanα。把 MM' = PM ∙ sinγtanα 代入 M'I'= M M'∙cotβ,得:M1I1= M'I'= PM ∙ sinγtanαcotβ。由 PM1=PM∙ cosγ,可知 PM1=PM∙ cosγ,把 PM1=PM ∙ cosγ 和 M1I1= M'I' = PM ∙ sinγtanαcotβ 代入 PI1=PM1-M1I1,得:PI1= PM∙ cosγ-PM ∙ sinγtanαcotβ,简化后,得:PI1= PM(cosγ-sinγtanαcotβ)。I1I″= M1M″,由M1M″= PM∙ sinγtanα 知,I1I″= PM∙sinγtanα。
图如 2-3 所示,M″S″=MS∙tanα'。将 α'=arctan (tanαsinγ)和 MS= PM∙sinγtanαsin(90-β) cos(arccot (tanαsinγ))/sin(β-arccot(tanαsinγ))代入M″S″=MS ∙tanα',得:M″S″= PM∙sinγtanαsin(90-β) cos(arctan (tanαsinγ))/sin(β-arc(tanαsinγ)) ×tanαsinγ,整理后得:M″S″ = PM ∙ sin2γtan2αsin(90-β) cos(arctan (tanαsinγ))/sin(β-arctan(tanαsinγ)),亦即在垂直纵投影图上沿地物长轴延伸方向的安全岩柱宽度 W 垂直2=L∙sin2γtan2αsin(90-β) cos(arctan(tanαsinγ))/ sin(β-arctan(tanαsinγ))。
同理,可以得到 N 点沿投影基线方向压覆矿体的垂直纵投影点 T″和沿视倾斜延深方向压覆矿体的垂直纵投影点U″。过S″、U″点做直线,分别于P I″ 和 P T″延伸线相交于 X″、Y″,编联 O-P-X″-Y″-O 压覆拐点,构成地面带状物受护边界在垂直纵投影图 (ABGH)上的压覆矿体范围。依 OPX″Y″为界,在垂直纵投影资源量估算图,对原地质块段进行分割计算和统计汇总,可获取压覆资源储量。
需要说明的是,当带状地物受护边界拐点沿地物长轴延伸方向的安全岩柱边界点超出矿体倾斜投影范围,则以矿体倾斜投影图的深部边界为安全岩柱边界。延伸PI、OT至矿体水平投影的底部边界线 EF 形成交点 X、Y,依次编联 O-P-X-Y-O 压覆边界点,即得到压覆矿体的水平投影边界范围;延伸 PI'、OT'至矿体倾斜投影图的底部边界线(EF)形成交点X'、Y',依次编联O-P-X'-Y'-O压覆边界点,即得到压覆矿体的倾斜投影边界范围;延伸 PI″、OT″ 至矿体垂直纵投影图的底部边界线 GH 形成交点 X″、Y″,依次编联 O-P-X″-Y″-O,即得到压覆矿体的垂直投影边界范围。
3 不规则带状物长轴方向斜交投影基准线(矿体走向)情形三
现实中,地表带状构(建)筑物或水体受护边界的平面形态往往是复杂的和不规则的,且其长轴方向常常与投影基线呈斜交关系。在充分了解地表物和矿体的空间叠置关系的基础上,并将其转化为空间三角函数关系,运用数学的方法,按照计算结果作图,从而实现压覆矿体范围的空间投影变换,继而正确地在垂直纵投影图上编联和圈定压覆矿体的边界范围,最后进行资源储量地质块段的分割计算和统计汇总,得到正确的压覆范围和压覆资源储量。对于复杂不规则带状地物而言,主要的研究方法就是化繁为简。即将复杂不规则带状地物,按其轮廓形态与走向变化,划简为若干段近似规则的地物,然后分段进行空间投影变化与作图,最后按照投影边界形态相似性原则,进行边界拐点的合理编联和压覆边界范围的正确圈定,解决复杂带状地物压覆陡倾矿体资源储量的分割圈算问题。具体可分为以下4个步骤。
(1)空间投影变换与作图前准备。①充分了解垂直纵投影图投影方位(矿体主体走向);②摸清地物类型与保护等级,明确地物受护边界范围;如果是河流或电站水库而言,按照现行的《建筑物、铁路、水体及主要井巷煤柱留设与压煤开采规范》之第68条规定,压覆边界为河流历史最高洪水位线或库区的千年校核洪水位线,确定水体压覆起算边界;③分析地表带状物的形态轮廓、长轴延伸总体方位、分段方位变化情况及其与投影基准线(矿体主体走向)的交角变化关系。在未开展空间投影变换与计算作图前,大致了解地物受护边界与压覆范围在水平/倾斜/垂直纵投影面上的基本形态轮廓与大致压覆范围,做到心里有数。
(2)分段化简。认真分析复杂不规则地表带状物平面形态展布特征,两侧分别确定起、终端点,并选取控制或影响边界形态的拐点(拐点选取越多,则越接近其真实形态),用线段依次编联起点、拐点和末端点,暂将不规则的地物边界线转化为若干条收尾衔接的规则线段。标定各线段的衔接顺序,并进行顺序编号,依次量取记录线段的长度、方位及其与矿体走向的交角,为空间投影变换计算做好准备。
(3)分段进行空间投影变换与作图。按照前述数学方法,依据具体计算结果,分段进行空间投影变换与作图,可分别得到地物受护边界拐点和各拐点对应的压覆点在水平/倾斜/垂直纵投影面上的投影位置。按照形态相似性原则,按顺序分别在水平/ 倾斜/垂直纵投影面上编联地物投影拐点和压覆拐点,得到地表地物保护范围在倾斜/垂直投影图的投影范围和其在水平/倾斜/垂直投影图压覆矿体范围。
由图4可知,M1为M、M'、M″在投影基准线(AB) 上的垂直投影点。由(33)式 PM1= PM×cosγ 可得 M1在投影基准线的位置,或由M向投影基准线做垂线,也可得 M1位置。同理,可知地物各受护边界拐点和对应各压矿边界拐点在垂直图上沿投影基准线的偏移距。因此,实际作图过程中,可首先将地表地物边界拐点和各拐点对应的压覆点的水平投影点,垂直投影至投影基准线(AB)上,依此获取各点在垂直纵投影图的水平距,再按前述的垂距公式,分别求得其在垂直纵投影图上的垂距,即可得到各拐点在垂直纵投影图上的位置。按照形态相似性原则编联地物投影拐点和压覆矿体的投影拐点,得到压覆矿体垂直纵投影范围。
(4)资源储量分割计算。在原垂直纵投影资源量估算图上,按照编联的压覆矿体边界,对原地质块段进行分割,并按各块度原估算参数进行分割计算和汇总,得到压覆的各级资源量;在平面图上,编联矿体水平压覆投影范围,并对拐点坐标进行统计列表,明确工程压覆/保护的地表边界范围。
4 讨论
4.1 情形一与情形二间的数学关联及验证
第一种情形是带状物长轴垂直于投影基准线,可用数学方式表达为 γ=90°,第二种情形是带状物长轴斜交投影基准线,可用数学方式表达为 0°<γ <90°。第一种情形可看做是第二种情形的特殊简单形式,这一点也可以从两种情形中对应计算公式间的数学关联看出。
当γ=90°时,将γ=90°代入情形二中的相应计算公式后可知,① 情形二中的 W 水平1=W 垂直1=L ∙ sinγtanαcotβ,可简化为情形一中的 W 水平1=W 垂直1=L∙ tanαcotβ;②情形二中的 W 水平2= L∙sinγtanαsin(90-β) cos(arctan(tanαsinγ))/sin(β-arctan(tanαsinγ)),可简化为情形一中的 L∙sinαsin(90-β) / sin(β-α); ③ 情形二中的 W 垂直2=L ∙ sin2γtan2αsin(90-β) cos (arctan(tanαsinγ))/sin(β-arctan(tanαsinγ)),可简化为W 垂直2=L∙ tan α sinαsin(90-β) / sin(β-α)。
上述的情形一与情形二间对应计算公式间的数学关联,也验证了压矿安全岩柱宽度计算公式推导结果的正确性。
4.2 空间投影变化过程中常见错误与计算作图的实践意义
在实际作图过程中,不少技术人员因不能正确理解压覆范围的空间投影变化,常常出现一种具有一定隐蔽性错误情形。往往将空间投影变换及作图过程简单化,从而导致压覆矿体边界形态与压覆范围的失真。一种易犯错误是既不考虑地表地物受护边界的平面形态,简单地以地物与矿体露头的交线代表整个地物的横截面形态,也不考虑带状地物与矿体投影基线的交角关系及其变化,错误地将其处理成与矿体投影基线垂直的特殊情形,最终导致压覆资源储量评估结果出现偏差,甚至是错误。对于具体的编图技术人员而言,要从空间投影变换的底层进行深入思考与正确理解,方能防范此类错误情形出现,维护压覆固体矿产资源估算评估的科学性、正确性和严谨性。
在理解空间投影变换本质的基础上,确定好投影基线和基准点,继而利用三角函数关系,以数学的方法,解决平面压覆拐点坐标及其平面压覆范围和在垂直投影资源量估算图上压覆范围。为方便空间投影变换与作图,实际压覆评估编图过程中,可充分利用 EXCEL 快速获取计算结果。如能在此基础上,借助计算机辅助制图,进行二/三维可视化显示与空间投影变换信息系统研建(徐平等,2013; 曹延飞等,2014),可进一步提高工作效率和作图的准确度,起到事半功倍的效果。
5 结论
(1)运用由简单到复杂的递进研究思路,利用空间投影变换过程中的三角函数关系,推导出水平投影图上,安全岩柱宽度沿投影基线方向的宽度 (W 水平1)和沿带状地物长轴延伸方向的宽度 (W 水平2 ),垂直纵投影图上,安全岩柱沿投影基线方向的宽度(W 垂直1)和沿带状地物长轴延伸方向的宽度(W 垂直2)的计算公式。
(2)为准确圈定带状构(建)筑物压覆陡倾矿体的水平投影边界范围和垂直投影边界范围,正确估算压覆固体矿产资源储量,提供了可靠的计算方法和正确的作图步骤,具有很强的实践意义和指导参考作用。避免在实际作图过程中,常因错误地理解空间投影变换,既不考虑地物平面形态的复杂性,也不考虑地物长轴方向与投影基线间的斜交关系,容易错误地将其处理为垂直于矿体走向的特殊情形,使得压覆范围与实际情况不符,最终导致资源储量评估结果出现偏差。
(3)在正确理解空间投影变化和数学计算方法的基础上,借助计算机工具,利用推导的计算公示,进行三维可视化计算成图软件开发,可节省繁冗的计算过程,快速实现压矿边界范围的空间投影变换和基于垂直纵投影图的压覆资源储量估算,提高作图效率和准确度,是该项工作今后重点研究方向。





