摘要
降雨是滑坡失稳的常见诱发因素之一,边坡降雨入渗是其稳定性分析的重要基础。本文采用一维 Richards方程描述裂隙中水分运移,二维Richards方程描述边坡土体渗流,以裂隙与边坡土体流量交换为联系,建立考虑裂隙影响的边坡降雨入渗数值模型。编制相应的计算程序,通过两个数值试验,说明了裂隙显著提高了土体渗透性,与不考虑裂隙影响的结果相比,入渗水量有较大增加,裂隙附近土体的基质吸力降低更为显著,当裂隙位于边坡后缘时,对边坡稳定性极为不利。
Abstract
Rainfall is one of the most critical factors which induces the landslide. The infiltration numerical simulation of slope is the foundation of slope stability analysis. In this paper, based on Richards’ equation, a new FEM numerical model is created by use of FEM which could solute the seepage field of slope and crack simultaneously. The exchange flux between above two filed are eliminated to avoid the definition of the flux. Furthermore, a finite element program for numerical simulation corresponding to the above model is coded, and two numerical experiments are carried out. It indicates that fractures improve the permeability of soil significantly is the important supply of infiltration. Fractures are important factors which should be considered in infiltration numerical simulation.
Keywords
0 引言
众所周知,降雨是边坡失稳的主要诱发因素,其不利影响可以概括为两个方面,一是降低了岩土体强度;二是产生了不利荷载,如增大岩土体容重,进而增大下滑力,又如产生顺坡向的动水压力。实际边坡中裂隙是降雨入渗的重要控制因素之一,例如马佳(2007)指出滑坡存在的大孔隙流、指流等现象,以及雨水沿滑坡后缘、两侧的张拉裂隙快速入渗的过程等,这些均大大增加了降雨入渗水量,是边坡稳定性评价时必须考虑的。
为能反映雨水的快速入渗,需要研究滑体中的优势流,特别是水分沿裂隙的入渗。土壤中的优势流及其对边坡稳定性影响的研究(马佳,2007)。
裂隙渗流在岩体渗流问题中得到广泛研究 (Reitsma and Kueper,1994;Persoff and Pruess,1995; 荣冠等,2007;刘晓丽等,2008;周创兵等,2008;荣冠等,2010)。刘博等(2016)结合黄土边坡裂缝法和非饱和土理论,建立了边坡破坏模型,推导出裂缝发育的黄土边坡在渗流力作用下的稳定性系数计算公式,并结合具体实例分析讨论了垂直裂缝尺度和渗流力对黄土边坡稳定性的影响。袁俊平等 (2016)为了揭示裂缝诱导各向异性对滑坡降雨入渗的影响规律,利用Seep/W软件进行了数值模拟分析,计算时:(1)将裂缝作为水头或孔压边界处理 (平扬等,2004),(2)将裂缝区域土体等效为不同于原状土的另一种材料,按照均质材料考虑,(3)对于宽深裂缝按已知边界处理,细浅裂缝按均化处理 (刘平,2007)。阙云等(2009)基于饱和-非饱和渗流理论研究了降雨条件下不同裂缝深度、裂缝开口宽度、裂缝分布位置、降雨强度和降雨持时等对裂缝性黏土边坡渗流场的影响,并进行了相应的稳定性评价。该学者在降雨边界处理上,当降雨强度小于土体表面的入渗能力时,计算入渗速率取为降雨强度,边界条件为 Neumann边界,反之,计算入渗强度为土体的入渗能力,边界条件为Dirichlet边界。
在膨胀土边坡稳定性分析中,人们逐渐认识到裂隙对雨水入渗以及稳定性的重要影响,并开展了一系列研究。袁俊平(2003)建立了膨胀土边坡裂隙网络入渗的数学模型用于研究裂隙对入渗的影响;殷宗泽和徐彬(2011)提出了一种以条分法为基础的近似反映裂隙影响的膨胀土边坡稳定性分析方法;王晓磊等(2012)以实际工程边坡为例,探讨了裂隙在推移式滑坡和牵引式滑坡中所起的作用; 殷宗泽等(2012)结合膨胀土边坡失稳实例探讨了裂隙所起作用。研究表明,裂隙对土质边坡稳定性往往起控制作用,包括加大入渗量和降低土体强度等作用。
上述研究表明,在考虑裂隙对边坡渗流影响的有限元数值模拟时(陈柏林等,2023;孙钱程等, 2023;屈小磊等,2024),当以总水头为求解变量时,可以将裂隙作为渗流场计算的边界条件,裂隙上所有点的水头值等于裂隙顶点高程;但是这种方法无法确定该边界条件的施加时间,所以通常从模拟开始即施加这一边界条件,计算结果偏于保守。另一种方法是将裂隙单独作为一种渗透性很大的材料,与边坡岩土介质统一作为求解域进行渗流模拟;但由于裂隙宽度相对与计算域而言很小,有限元网格剖分时裂隙附近的单元尺寸必须很小,极大增加了计算开销,还可能导致网格形状畸形、甚至网格剖分失败,导致计算工作无法进行。
因此,本文拟采用一维 Richards 方程描述裂隙中水分运移,二维Richards方程描述边坡土体渗流,以裂隙与边坡土体流量交换为联系,建立考虑裂隙影响的边坡降雨入渗数值模型,为探讨降雨诱发滑坡的机理奠定基础。
1 基本理论
数值模型所涉及的基本理论及初边界条件叙述如下。
1.1 降雨时坡体渗流的控制方程和定解条件
坡体渗流可由 Richards 方程(Richards,1931) 描述:
(1)
式(1)中,C = ∂θ/∂φ(m-1);H 为水头(m);H = y + φ,y为位置势(m),非饱和时φ为基质吸力(m),饱和时 φ 为压力水头(m);Kx,Ky 为 x、y 方向的渗透系数(m/s);fP 为裂隙端点对坡体渗流的补给,类似于点源(1/s);其他符号同前。
初始条件为:
(2)
为简洁起见,边界条件只考虑坡体入渗强度 I (在Γ1上,m/s)和裂隙补给强度fL(在Γ2上,m/s),可表示为:
(3)
(4)
式(3~4)中,fL为裂隙对坡体补给强度(m/s)。
1.2 降雨时裂隙渗流的控制方程和定解条件
假设滑体上的裂隙也被多孔介质填充,相对滑体而言,它们具有更大的渗透性,假定渗流沿裂隙深度方向进行,单位宽度上采用一维 Richards 方程描述裂隙中水分运移:
(5)
式(5)中,Kf 为裂隙渗透系数(m/s);s 为裂隙长度(m),其他符号同前。
初始条件为:
(6)
边界条件为(设裂隙长度为S):
(7)
式(7)中,f为裂隙入渗强度(m/s)。
裂隙渗流也可用其他控制方程描述,例如运动波模型,此时可仿照本文后面构建联合求解模型的思路,建立类似的联合求解模型。
2 数值模型的构建
根据坡体渗流、裂隙渗流的控制方程和边界条件,采用Galerkin加权余量法,可建立相应有限元求解模型。联合求解模型构建的总体思路是,将坡体渗流场划分单元,则坡体渗流单元的边可作为裂隙渗流场的单元;然后根据有限元数值模型的特点,消去两场间的流量交换。当网格节点统一后,裂隙单元节点的水头与坡体单元同编号节点的水头相同。
根据控制方程及其边界条件,采用 Galerkin 法可得边坡岩土介质渗流有限元模型如式(8)所示,本文加入了关于裂隙渗流的考虑:
(8)
式(8)中,[ D ],[ S ],{ P } 是由相应单元矩阵 [ D ] e,[ S ] e,{ P } e 集成而得。各单元矩阵的元素分别为:
dij = ∫ [ Bi ] T [ K ] [ Bj ] dxdy,其中, [ Bi ] = [ ∂Ni /∂x,∂Ni /∂y ],[ K ]为渗透张量,Ni 为形函数;sij = ∫∫CNiNjdxdy;pi = ∫NiI cos θidl + fpmj + ∫Ni fL ds,其中, fpmj 为裂隙在节点 mj 进入坡体的流量,∫NifL ds 为裂隙沿边s进入坡体的流量。
裂隙渗流的有限元格式为:
(9)
式(9)中,[ E ],[ G ],{ Q }是由相应单元矩阵[ E ] e,[ G ] e,{ Q } e 集成而得。各单元矩阵的元素分别为:
将式(8)和(9)左右对应相加,可消去裂隙渗流与坡体渗流间的流量交换,即得求解数值模型:
(10)
式(10)中,[ M ],[ S ],{ R }由相应单元矩阵[ M ] e , [ S ] e,{ R } e 集成。其元素分别为:mij = dij + eij;sij = sij + gij;ri = ∫NiI cos θidl。
为最终将式(10)转换为{ H }的线性方程组,可将式(11)写为向后差分格式:
(11)
3 数值试验
本节根据所建模型,编制相应计算程序,对图1所示边坡开展降雨入渗数值模拟。图2中,自 B 点右侧设4条竖直裂隙(虚线表示),间距1 m。
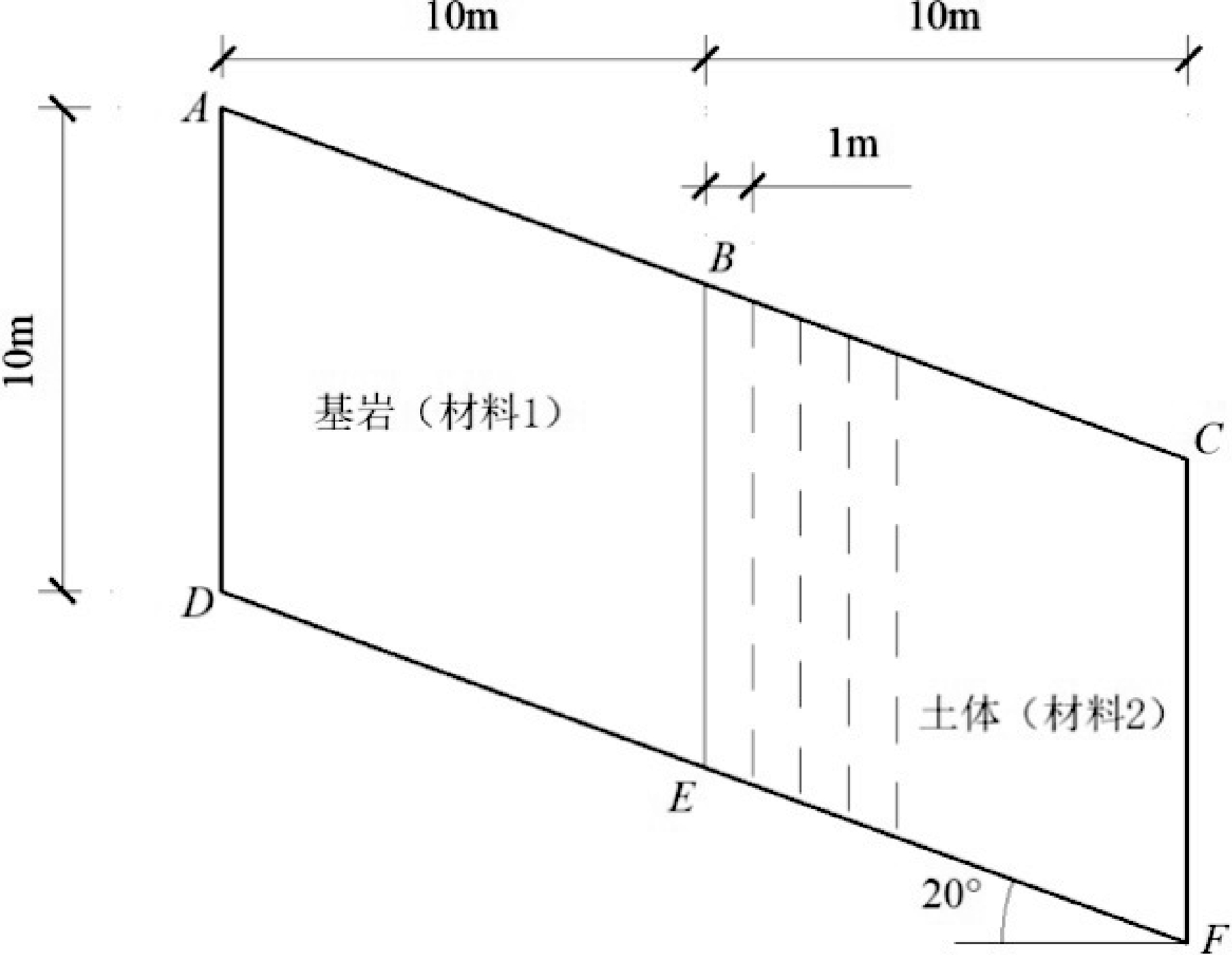
图1几何模型
3.1 数值试验1
本试验中,边坡几何模型尺寸分别为:H1=10 m, L1=L2=10 m。本算例只考虑F1的影响。
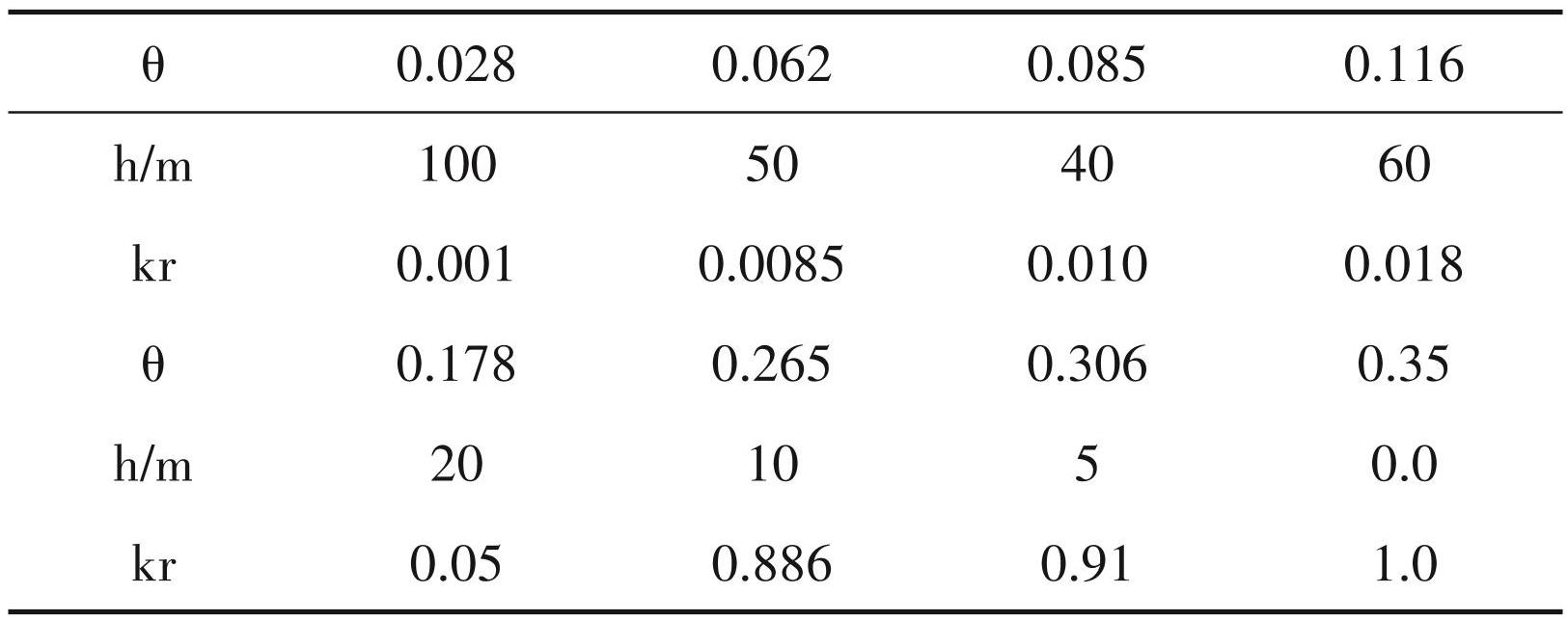
基岩饱和渗透系数为10-8 cm/s。土体饱和渗透系数为 10-5 cm/s,土体的 SWCC 与渗透性函数见表1。裂隙渗透系数为土体的 100 倍,不考虑非饱和特性。
边界条件:边 ABC为降雨边界,雨强 100 mm/d,持续10 d;其余边界不透水。
表1土体SWCC与渗透性函数
有限元单元网格水平长1 m,高0.25 m,形状同几何模型,为平行四边形。
当降雨边界上节点水深大于 0 时,将降雨边界改为0水深边界。坡体入渗量的对比如图2所示。

图2坡体入渗量对比
在第 10 d 时最终入渗量依次是:考虑裂隙为 9.24 m3,不考虑时为 5.61 m3。可见考虑径流时入渗量大为增加,增幅约50%。
考虑径流和裂隙、只考虑裂隙情况下的第 10 d 时边坡渗流场(压力水头)等值线见图3,只画出了边坡土体部分,图中虚线为裂隙。
由图3可知,由于裂隙很大的渗透性,裂隙附近压力水头明显较低,意味着裂隙附近土体基质吸力降幅较大,土体强度降低较大;同时土体含水量较高,土体所受重力较大,意味着降雨初期边坡处于顶部加载状态,不利于边坡稳定。
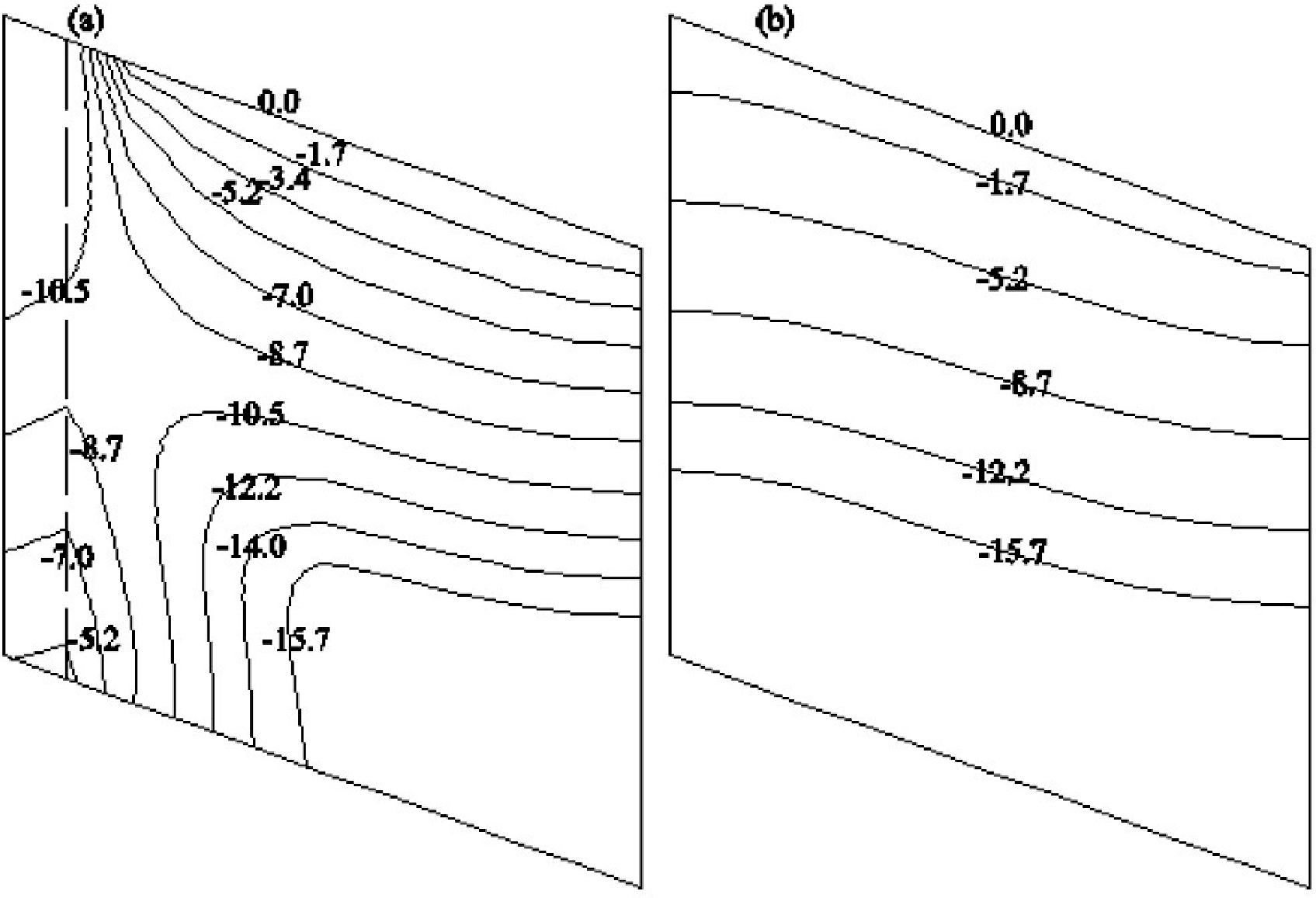
图310 d时渗流场对比(单位:m)
a—考虑1条裂隙;b—不考虑裂隙
3.2 数值试验2
本试验中边坡几何模型尺寸、材料参数、边界条件同试验 1。计算时同时考虑径流和裂隙的作用。本试验主要对比裂隙条数对入渗量以及渗流场的影响,即考虑裂隙F1,裂隙F1、F2,裂隙F1、F2、 F3,裂隙F1、F2、F3、F4共4种情况。
坡体入渗量的对比如图4所示。在第10 d时最终入渗量依次是:1 条裂隙为 9.36 m3,2 条裂隙为 10.3 m3,3条裂隙为10.9 m3,4条裂隙11.9 m3,近似成比例增加。

图4不同条数裂隙的对入渗量
由不同条数裂隙在第10 d时的渗流场(图5)可知,裂隙条数越多,坡体入渗雨量越大,当遇到相对隔水层时,将会出现局部饱和区域(随裂隙条数增加范围增大),这将降低土体参数,同时也产生顺坡向的超孔隙水压,对边坡稳定不利。
4 结论与展望
(1)基于Richards方程依托有限元法,通过消去坡体渗流、裂隙渗流间的流量交换,建立了两场联合求解模型。
(2)编制了相应程序,开展了数值试验,说明了裂隙对边坡渗流场具有重要影响,定性分析了对边坡稳定性影响。
(3)本文模拟的边坡中存在一维垂直裂隙情形,与实际情况存在一定的差异;尤其当边坡存在多条垂直裂隙时,其他方向的裂隙也将影响边坡渗流,将在今后进一步开展研究。
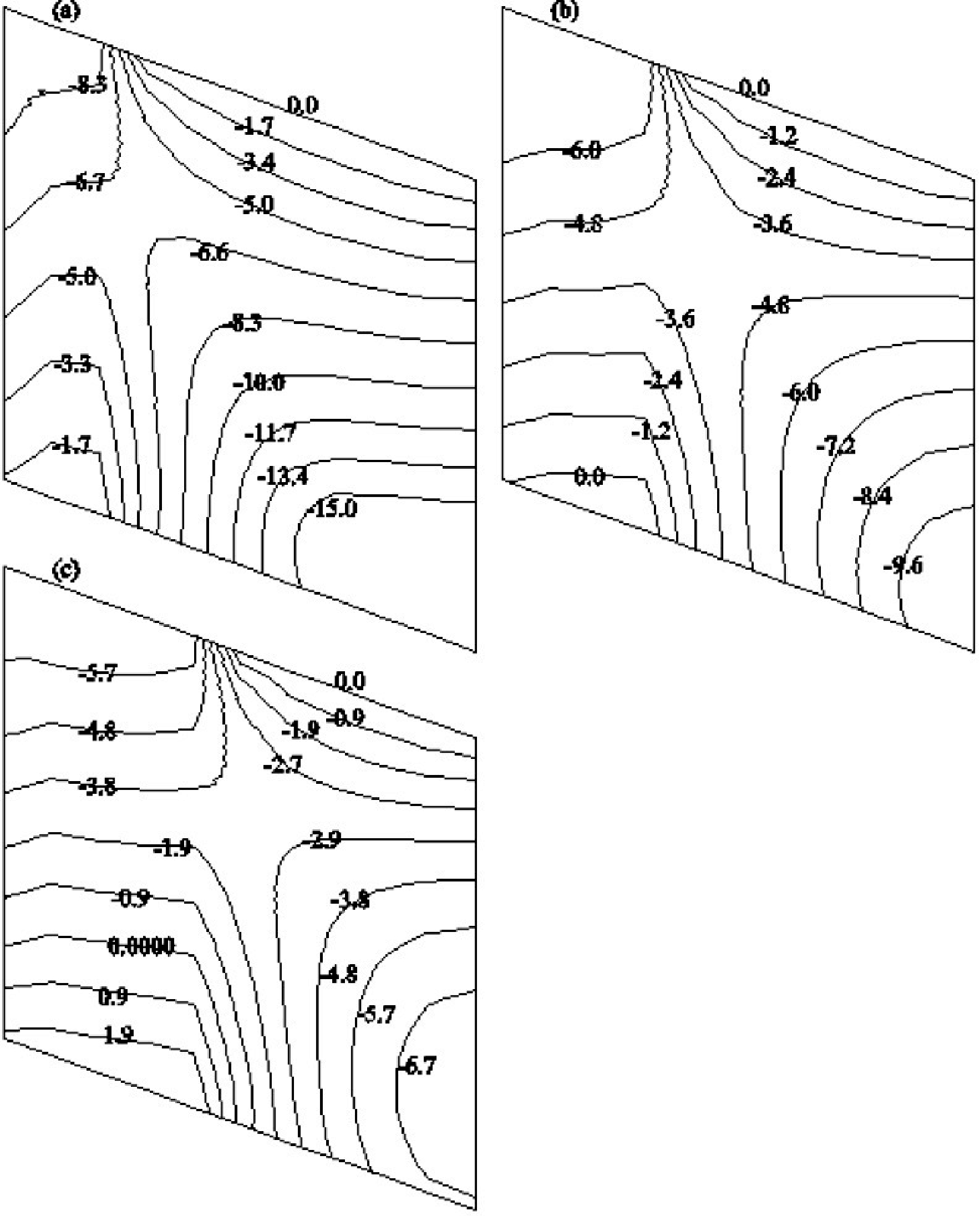
图5不同裂隙条数时的渗流场(单位:m)
a—2条裂隙;b—3条裂隙;c—4条裂隙





