摘要
作为常用的支护结构,预应力锚索可划分为拉力型集中型、压力集中型、拉力分散型、压力分散型几种常用形式,拉力型锚索和压力型锚索由于构造不同,受力机理和刚度也不相同,而刚度是控制变形的关键因素,锚索刚度大变形小,反之变形大。本文根据拉力型和压力型锚索受力机理不同分别计算两类锚索刚度,最终在实际项目中采用压力型锚索刚度进行支护结构设计,并与支护结构实际监测变形对比,旨在为压力型锚索采用变刚度调平设计是安全、合理、可行提供依据,也为今后不同类型锚索设计提供了参考。
Abstract
As a commonly used support structure, prestressed anchor cables can be divided into several common forms: tensile concentrated type, pressure concentrated type, tensile dispersed type, and pressure dispersed type. Due to their different structures, tensile anchor cables and pressure anchor cables have different stress mechanisms and stiffness, and stiffness is the key factor in controlling deformation. The stiffness of the anchor cable is large, and the deformation is small, and vice versa. This article calculates the stiffness of two types of anchor cables based on the different stress mechanisms of tension type and pressure type anchor cables. Finally, in practical projects, the stiffness of pressure type anchor cables is used for support structure design, and compared with the actual monitoring deformation of the support structure. The aim is to provide a basis for the safety, rationality, and feasibility of using variable stiffness leveling design for pressure type anchor cables, and also provide reference for the design of different types of anchor cables in the future.
Keywords
0 引言
作为常用的支护结构,预应力锚索可划分为拉力集中型、压力集中型、拉力分散型、压力分散型几种常用形式,拉力型锚索和压力型锚索由于构造不同,受力机理和刚度也不相同,而锚索刚度是控制变形的关键因素,锚索刚度大变形小,反之变形大 (图1)。本文采用拉力集中型锚索和压力集中型锚索为例进行刚度比较研究。
1 锚杆刚度计算方法
锚杆刚度计算方案目前通常按照《岩土锚杆与喷射混凝土支护工程技术规范(GB50086-2015)》推荐计算方式
(1)
式(1)中 kH—支护结构水平支点刚度系数(kN/ m2);E—锚杆杆体弹性模量(kN/m2);A—锚杆杆体横断面面积(m2);Lft —锚杆杆体自由长度(m),对于拉力型锚杆取其自由段与 1/3 锚固段长度之和,对于荷载分散型锚杆取最前端的单元锚杆杆体的非黏结长度;s—锚杆间距(m);θ—锚杆倾角(º)
为方便比对,不考虑锚杆间距 s,公式(1)转化为式(2):
(2)
不难看出公式中杆体弹性模量、杆体截面积、自由段长度以及锚索倾角均对锚杆刚度有不同程度的影响。
2 不同类型锚杆刚度对比
以抗拉强度标准值 1860 MPa,抗拉强度设计值 1320 MPa,公称直径 15.24 mm,杆体截面积 A= 0. 00014 m2,杆体弹性模量 Es=195000 MPa 的钢绞线分别制成拉力集中型和压力集中型锚索,锚杆倾角均为0度,相关参数如下。
表1不同类型锚杆刚度对比
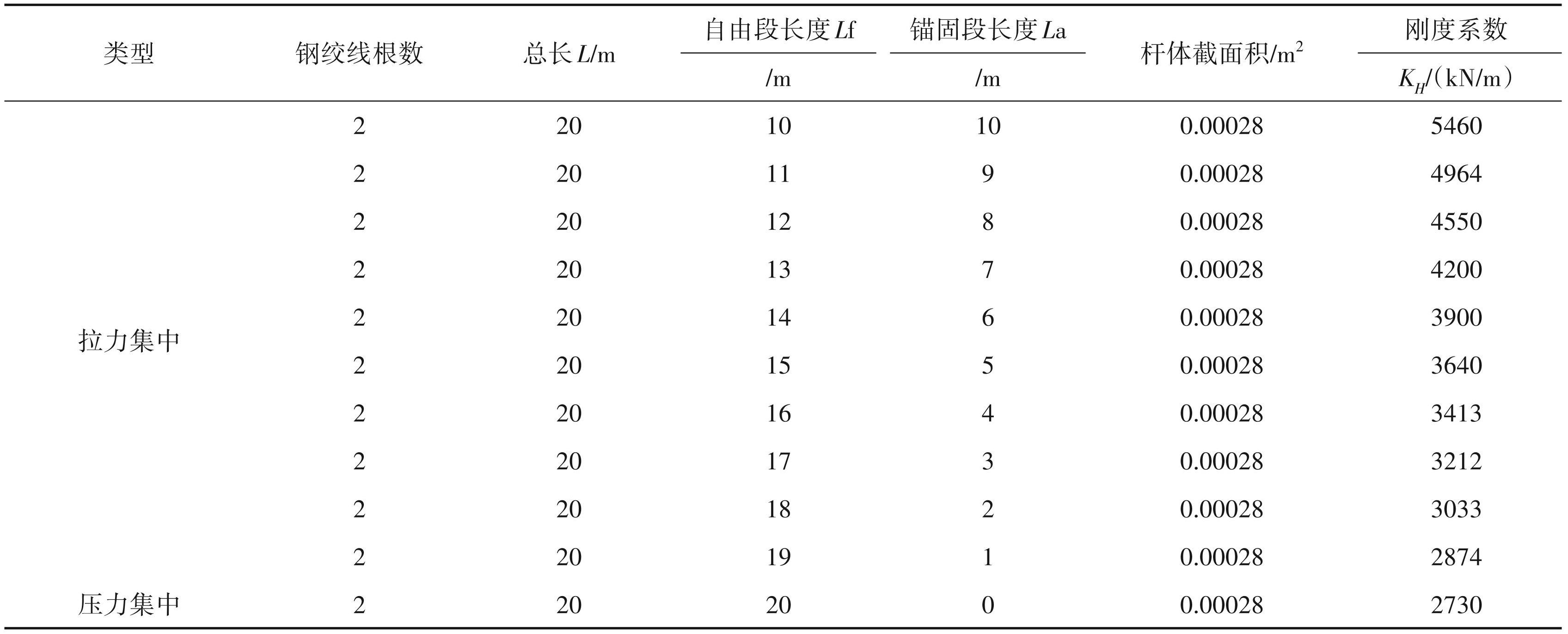
根据式(2)计算锚杆刚度系数,显而易见,随着锚杆自由段的不断变长,锚杆锚固段减至0,锚杆成为全长无黏结的压力型锚杆,锚杆刚度系数不断减小,压力集中型锚杆刚度仅为拉力集中型锚杆刚度的大小的一半,因此可以简单认为在受到同等大小拉力情况下,压力集中型锚杆控制变形的能力仅为拉力集中型锚杆控制变形能力的一半。
锚杆自由段长度、锚固段长度对锚杆刚度的影响:
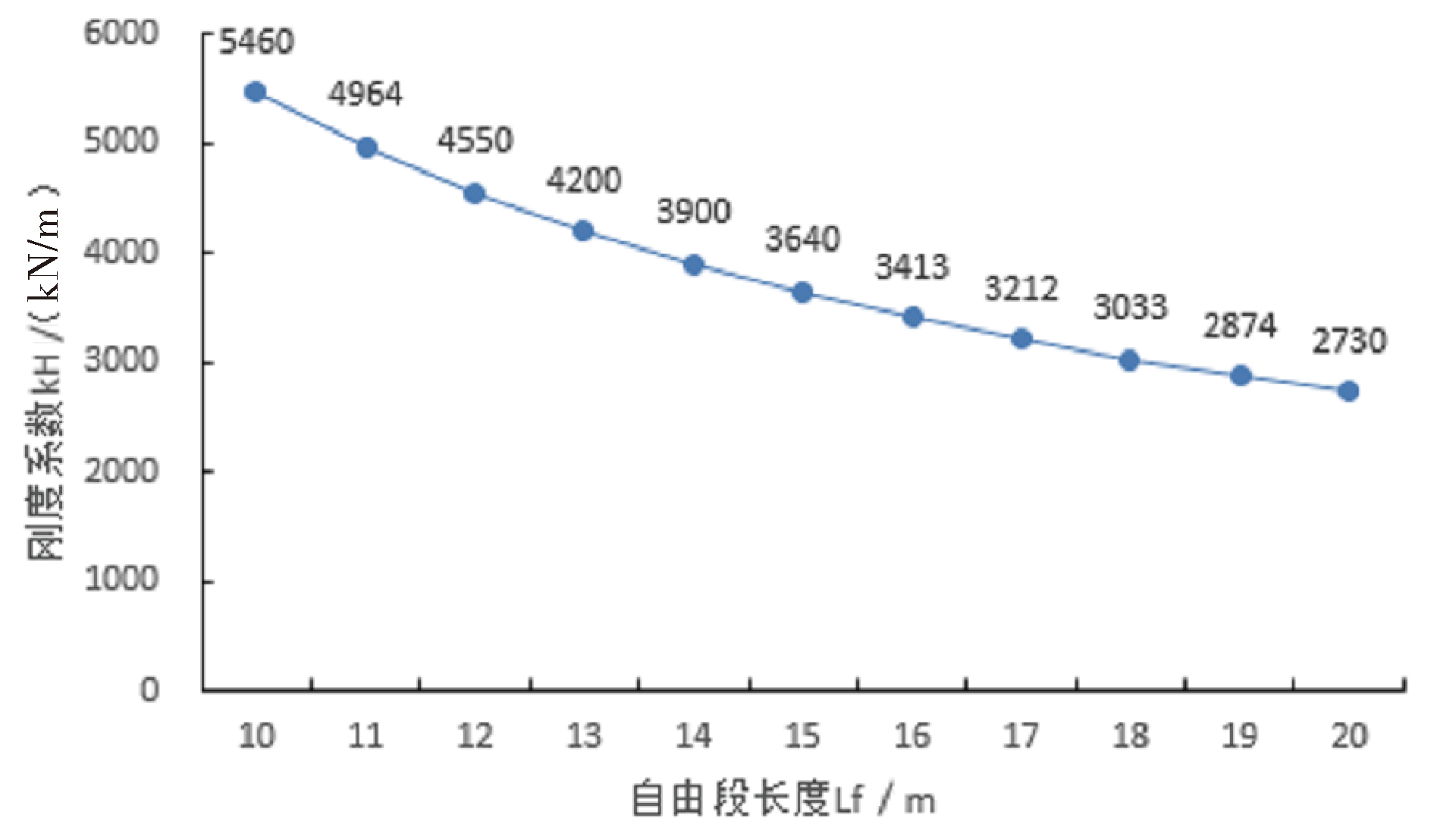
图1不同自由段长度与锚杆刚度关系
3 实际案例分析
3.1 项目概况
项目位于昆明市五华区一环内,北侧紧邻市内主干道,车流量大,东侧紧邻部队老旧建筑,差异沉降敏感,南侧紧邻部队自建 25 层(-3F)高层住宅。采用桩+锚索支护的剖面位于场地东侧,该剖面某紧邻3~6层砖混建筑,基础形式为浅基础,地下室外墙距离红线最近3.4 m(图2)。
3.2 地质情况
3.2.1 工程地质条件(表1)
①层杂填土:湿度小,结构松散,主要由砼块,碎砖块、碎石夹黏性土组成,土质不均匀。
表2土层力学性质指标

注:*表示为经验值。
②层含黏性土砾砂:饱和,中密为主,部分密实,砾石主要呈次棱角—次圆状,母岩成分为石英岩、玄武岩等,呈强—中风化状,粒径为 2~20 mm; 具中偏低压缩性,含25%~40%的黏性土。

图2典型设计剖面
②1层—黏土:可塑状态为主,局部硬塑或坚硬状态,局部夹约 10% 的砾砂,粒径 2~20 mm,母岩为强—中风化砂岩、玄武岩等,略有光泽,干强度及韧性中等,以中压缩性为主,局部高压缩性。
②2层粉土:湿度大,密实为主,部分中密,局部夹 20~40 cm 的薄层粉砂,干强度低,韧性差,具中压缩性,土质均匀性一般,黏粒含量5.3%~25.8%,平均值为 13%。
③层粉土:湿度大,密实为主,局部中密,摇震反应轻微,局部含 20~40 cm 的薄层粉砂,干强度低,韧性差,具中压缩性,土质均匀性一般,黏粒含量6.5%~28.3%,平均值为17.2%。
③1 层黏土:湿度小,硬塑状态为主,局部可塑或坚硬状态,干强度及韧性中等,具中压缩性,物理力学性质较好。
④层红黏土:湿度小,以可塑状态为主,局部硬塑状态,局部含少量强风化灰岩角砾,粒径 5~30 mm,土质结构相对疏松,干强度高,韧性中等,具中压缩性。
3.2.2 水文地质条件
地下水类型主要为上层滞水、孔隙型潜水及基岩裂隙型潜水。上层滞水主要赋存于杂填土中;孔隙水型潜水主要赋存于砾砂层和粉土层中。上层滞水主要赋存于表层杂填土层中的孔隙中。主要受大气降水和地表。
孔隙型潜水主要赋存于②层含黏性土砾砂、 ②2层粉土、③层粉土中,该含水层孔隙连通性相对较好,透水性强,具微承压性,水头 0.9~3.6 m。孔隙型潜水主要大气降水的补给,该层水位埋深在地面以下2.1~6.4 m。
3.3 剖面设计情况
该剖面开挖深度 15.4 m,采用 φ1200 支护桩桩长 L=31 m@1.8 m,基坑安全等级一级,原设计采用 5道拉力集中型预应力锚索。
按拉力集中型锚索设计时,各排锚索刚度按式 (2)计算见表3,按以上刚度计算支护结构整体变形见图3。
在采用拉力集中型锚索时,锚索刚度大,桩锚支护结构桩顶位移仅 5.44 mm,桩身最大位移仅 26.19 mm,位移控制情况较好,但在最不利工况(开挖至基坑底)时,锚索最大受力可达 520~610 kN,锚索在自由段与锚固段结合处受力较大,结合经验在该种土层中一般拉力集中型锚索极限抗拔承载力为 550~650 kN,锚索的抗拔安全系数不满足规范要求,抗拔安全储备较低(表4)。
表3拉力集中型锚索设计参数
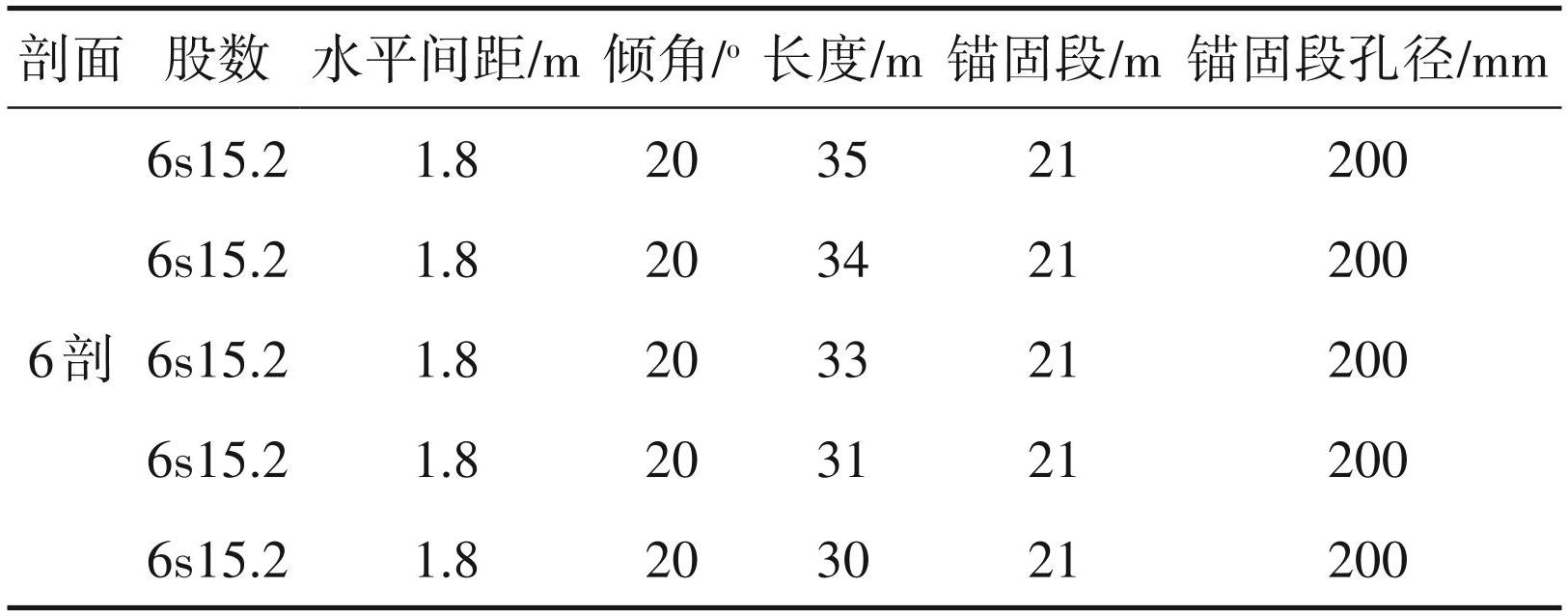

图3采用拉力集中型锚索支护结构变形
表4拉力集中型锚索刚度系数计算

为解决锚索承载力不足,安全储备较低的问题,将5排预应力锚索均调整为压力分散型锚索,锚索分 3 个锚固单元,每个锚固单元长 7 m,每单元锚索 2 束钢绞线。由于压力型锚索全长无黏结,全长可视作自由段,按式(2)分析可知,锚索的刚度必将大幅下降,各排锚索刚度按式(2)计算如表5,按以上刚度计算支护结构整体变形见图4.
表5压力分散型锚索设计参数及刚度

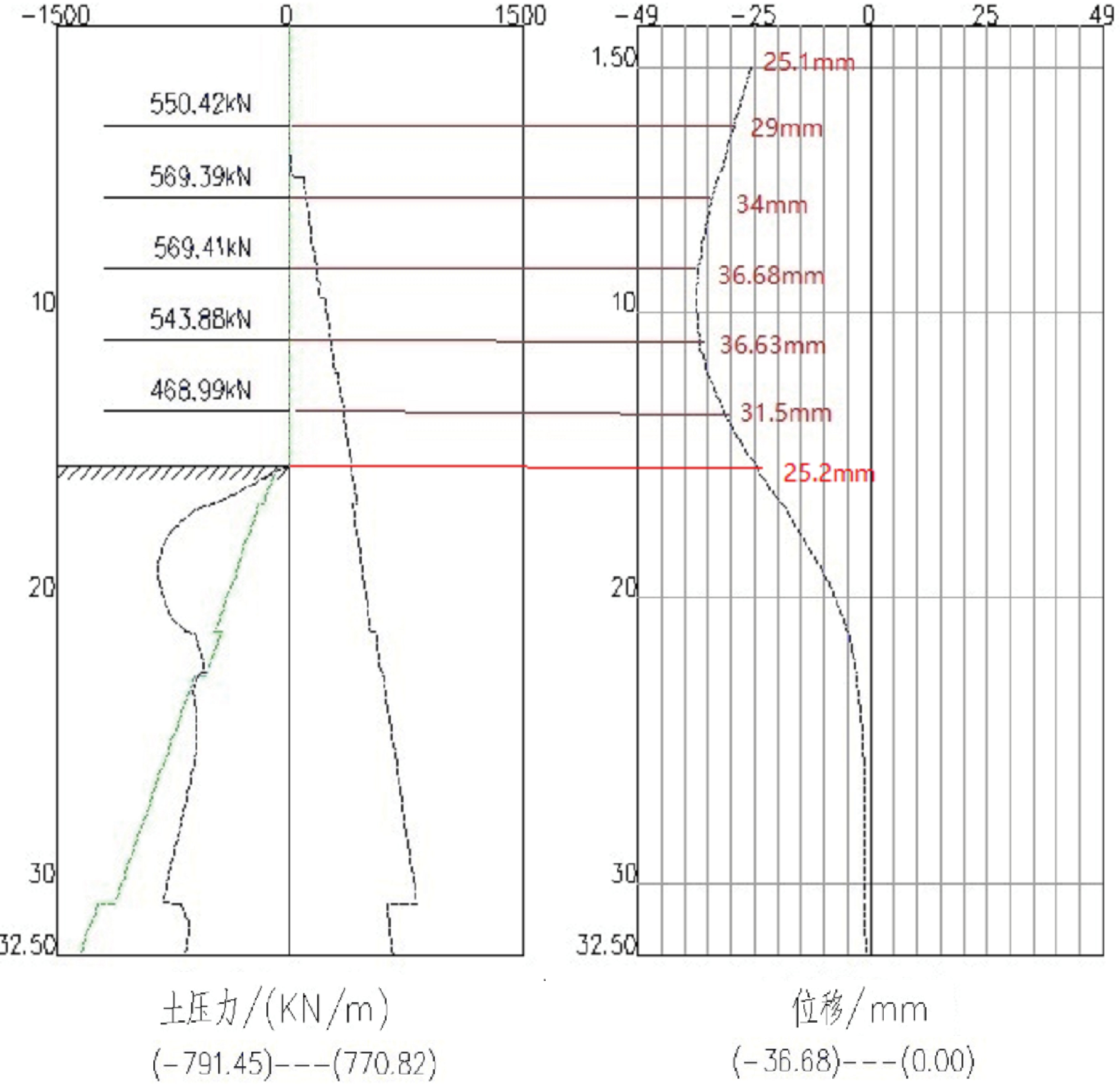
图4采用压力分散型锚索支护结构变形
4 结论
(1)采用压力分散型锚索刚度代入设计,支护结构的整体水平位移均大于采用拉力集中型锚索刚度代入设计。
(2)在该剖面中间位置桩身布设了7个监测点,分别位于(冠梁顶-1.5 m/-3.5 m/-6 m/-8.5 m/-11 m/-13.5 m/基底-15.4 m)实际变形监测值与采用压力分散型锚索刚度设计时非常接近(图5)。
(3)通过以上变形数据不难看出,本研究压力分散型预应力锚索采用变更度调平设计是安全、合理、经济的(图6、图7)。
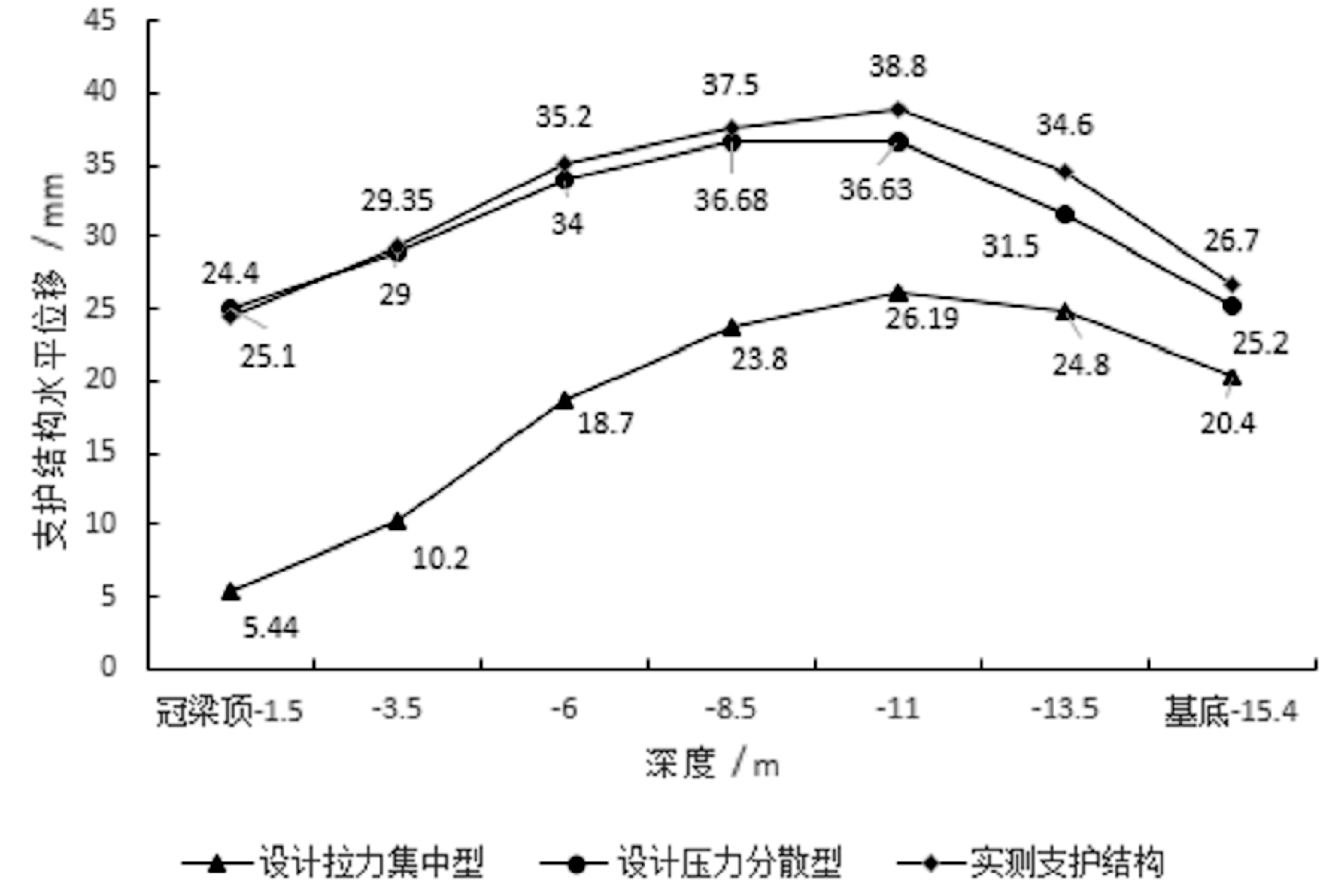
图5各种情况下支护结构位移

图6开挖到基坑底照片
5 结论
本文根据不同类型锚索构造及受力机理的不同,分别计算了拉力型和压力型锚索刚度,并通过实际应用。得到以下结论:
(1)不同类型锚索根据其构造及受力机理不同其刚度也是不尽相同的,相同长度的压力型锚索的刚度小于拉力型锚索。

图7开挖到基坑底照片
(2)不同类型锚索采用不同刚度进行设计是安全、合理的。
(3)不同类型锚索采用不同刚度进行设计,支护结构理论变形量与实际监测变形量相近。
(4)为今后相同类型锚索刚度、支护结构变形提供了一定参考。











