摘要
针对大范围扫描地质图地理配准中存在的地图畸变复杂、转换参数描述与控制点选取困难的问题,提出了一种边缘检测和分区配准相结合的扫描地质图配准算法。该算法使用Canny检测和Bessel函数进行图廓降噪,再由最小二乘法拟合图廓并校正畸变,最后根据图像变形情况使用Delaunay三角网分割图像,逐一解算各区域配准参数,拼接重建精确的地理配准图像。结果表明:(1)图像畸变校正后,40个图廓点横向、纵向平均偏差分别降低52.90%、77.81%;(2)相比传统的相似多项式、仿射变换、三阶多项式、样条函数配准,本文方法点要素配准精度分别提高了22.64%、22.07%、14.26%、1.76%,线要素配准精度提高了 49.73%、51.25%、37.01%、26.54%,表明本文方法配准精度更高,实现了顾及畸变的高保真精确地理配准。
关键词
Abstract
Aiming at the problems of complex map distortion, difficult description of transformation parameters and selection of control points in geographic alignment of large-scale scanned geological maps, an alignment algorithm for scanned geological maps combining edge detection and zonal alignment is proposed. The algorithm uses Canny detection and Bessel function for contour noise reduction; then the least squares method is used to fit the contour and correct the distortion; finally, according to the deformation of the image, the image is segmented by Delaunay triangular mesh, and the alignment parameters of each region are solved one by one to reconstruct the accurate geo-aligned image by splicing. The results show that: (1) After the image distortion correction, the average horizontal and vertical deviation of 40 contour points are reduced by 52.90% and 77.81%, respectively; (2) Compared with the traditional similar polynomials, affine transforms, third-order polynomials, and spline functions, the accuracy of the point elements of this paper's method improves by 22.64%, 22.07%, 14.26%, and 1.76%, and the accuracy of line elements improves by 49.73%, 49.73%, and 1.76%, respectively. The accuracy is improved by 49.73%, 51.25%, 37.01%, and 26.54%, which indicates that the method in this paper has higher alignment accuracy and achieves high-fidelity accurate geographic alignment considering aberrations.
0 引言
地质图是地质勘查工作的重要数据源,矿区地质图所表达的地质特征是遥感地质解译、地球化学勘查、地球物理勘探、野外地质调查等工作所需的的先验知识和验证依据。目前国内已基本实现了数字化制图,但一些欠发达地区,如作为矿产资源安全战略保障的非洲(任军平等,2021;孙凯等, 2022;丁俊等,2024),还经常需要将当地地质图由扫描、拍照形式转化为不含空间参考信息的图像,要将扫描图像与其他勘查数据匹配、融合进行信息综合时,必须对其进行地理配准,当图幅范围较大时,地理配准过程中会存在坐标转换参数描述复杂和控制点选取困难的问题(陈国旭等,2010;齐风友,2024)。同时,图纸由于干燥、长期存放不当造成的图纸变形以及纸质图扫描过程中引入的误差,导致图像存在一定程度的畸变,降低了地理配准精度,从而无法实现与其他数据精确匹配。因此提高扫描地质图的地理配准精度仍然是地质勘查中的重要问题。
要实现精确的地理配准,首先要纠正图像畸变。早期校正图像畸变校正策略主要关注于适应畸变情况的数学模型校正,部分学者使用栅格多项式拟合模型进行畸变校正,在保证校正精度的同时避免了校正后图像像素缺失的现象,但是存在模型复杂和通用性差的缺点(申学林等,2023)。近年来计算机视觉技术发展迅速,受此启发,基于计算机视觉算法进行图像畸变校正的方法被提出(张红霞等,2018;Ri and Wang,2019;李唐薇等,2020;He et al.,2023;张晨阳等,2023),出现了许多基于图像检测算法的图像畸变校正方法,对二值化标定后的图像进行边缘检测并计算出点位坐标从而根据交点坐标结合对图像进行校正,这种方法可以有效利用图像边缘轮廓信息,具有校正精度高、解算难度低的优点。
校正图像畸变以后,需要获取位置准确、分布合理的地理配准控制点。传统选择控制点的方式多为人工标定控制点,这种方式虽然操作简单,但是会引入操作误差且工作量大,自动化解算和描定控制点位置可以得到更高的点位精度(徐阳,2021; 王艳东等,2022)。近年来许多学者将计算机视觉理论和滤波函数、梯度等方法引入求解控制点位置 (陈文艺等,2020;谈杰等,2022),有效降低弱纹理区域和边界的误匹配率,提高了控制点选取精度。
总而言之,图像畸变校正和获取准确地理配准控制点的目的是为建立准确的扫描图与地表空间映射关系。目前尚难以在物理意义上实现地图与真实地表之间的像素级一一对应,实际应用中通常是根据控制点坐标解算变换函数参数来实现地理配准。然而在图幅较大时地图与地表空间对应关系难以用一个函数系进行表达,于是有学者使用分区校正的策略,基于图的分割算法,对每个区域单独解算变换函数,逐一配准,在提高算法速度的同时取得了比整体纠正法更高的配准精度(赵小川等,2009;Jin et al.,2019;郭昕刚等,2022;王岩等, 2023);李佳莹等(2020)以相机主点为中心按距离加权值进行分区校正,结果表明在分为两区域和三区域情况下,偏移量误差比传统不分区方法分别降低14.7%和29.93%;一些学者使用Delaunay三角网进行图像分割并且在此基础上进行配准(姜三和江万寿,2020),结果表明与传统匹配算法相比,分区配准算法能有效地提高图像的匹配精度。然而,实际工作中由于原图畸变和控制点选取精度不高,分区配准的实际效果会受此影响。实际项目工作中发现地图配准误差将直接影响最终遥感地质勘查工作精度。因此,在顾及图像畸变情况下,首先对扫描地质图进行畸变校正,再通过边缘检测算法计算控制点位置信息,避免了人工选点带来的误差; 而后引入Delaunay三角网对扫描图进行分区配准与重建,实现高精度的扫描图地理配准;最后基于图廓点及图内点、线要素开展多因子评价,并对比传统地理配准模型对算法性能进行评估。
1 实验数据与配准方法介绍
本文使用刚果共和国南部Mpassa、Moubiri、 Mindouli矿区扫描地质图进行配准实验,地质图覆盖范围位于4°10'~4º25'S,14°03'~14°28'E,地质图比例尺为1∶50000,覆盖面积1713.32 km²;扫描栅格影像分辨率为6.5 m×6.5 m,栅格行数为4929、列数为10679。由于图纸变形、扫描过程中引入的误差等原因,图像存在复杂的畸变形式,如图1所示,图像左下区域主要存在切向畸变,表现图像朝同一方向发生位移;在图像右侧区域主要存在径向畸变,表现图像偏移方向汇聚于某一点。
图2所示为配准流程,具体步骤为:①使用 Canny边缘检测算法提取扫描图图廓再根据Bessel 函数、最小二乘法进行降噪和标准图廓拟合;②利用图廓点理论位置对扫描图在图像坐标系下进行畸变校正;③基于分区校正的思想引入Delaunay三角网,以图廓点偏移方向延长线交点附近可计算理论坐标的网格点作为顶点构建Delaunay三角网,依据变形情况对扫描图进行分区并逐一解算配准参数,对各三角网块进行地理配准与重建,从而实现扫描地图的精确配准。
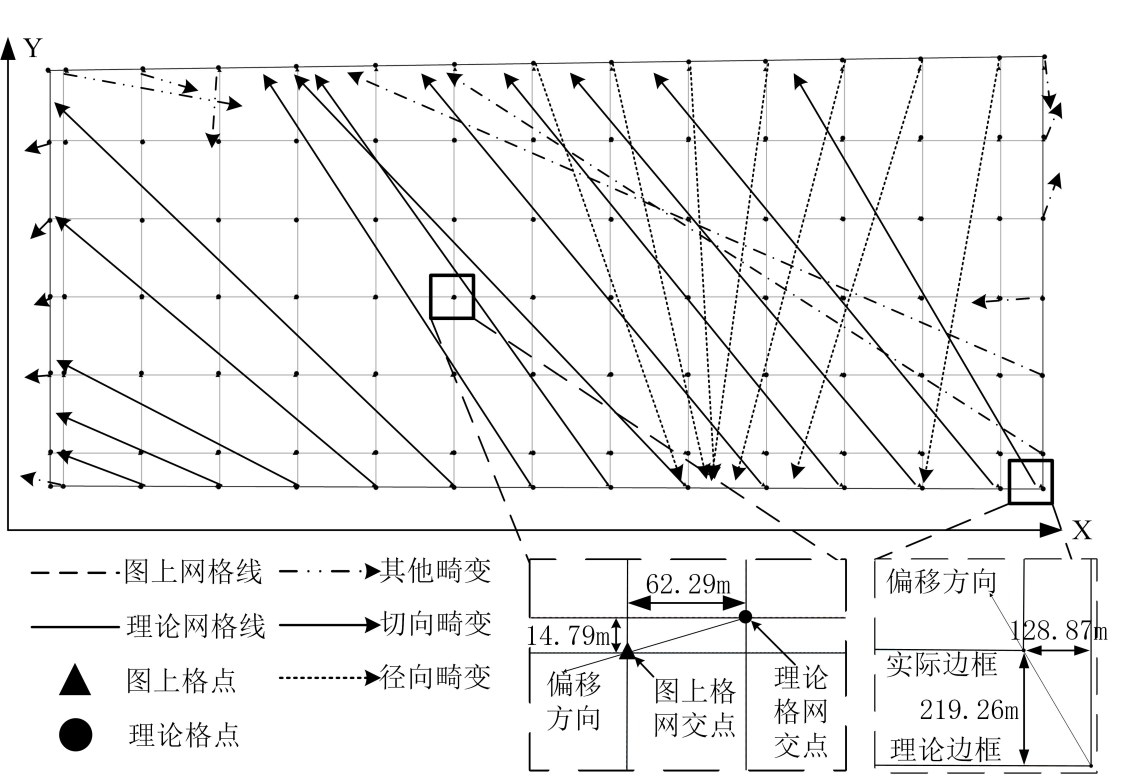
图1图像变形情况示意
本文精度验证数据分为2个类别:点要素和线要素。点要素包括理论坐标已知的40个图廓点和真实坐标已知的26个图上控制点,线要素使用了经过几何精校正的Sentinel-2A卫星影像,空间分辨率为10 m,从中提取了图上出现的道路、河流等线状要素。
2 地质图畸变校正
地质图畸变校正目的是校正扫描图各种复杂畸变,为后续的精确地理配准提供较为准确的扫描图件与控制点信息。校正过程主要涉及3个重要环节:Canny边缘检测、Bessel函数降噪与最小二乘拟合、畸变校正。
2.1 Canny边缘检测
Canny边缘检测是目前应用最为广泛的边缘检测算法之一(张岩等,2020;Jing et al.,2022)。算法首先使用滤波平滑纹理较弱的非边缘区域,这里采用二维高斯函数的导数(李静等,2021):
(1)
式(1)中,x和y为当前位置相对于检测区域中心的坐标,σ是尺度因子。而后计算图像边缘梯度,选出位于边缘位置的像素。以像素(xy)在x方向与 y方向上的偏导数值之和计算梯度,公式为:
(2)
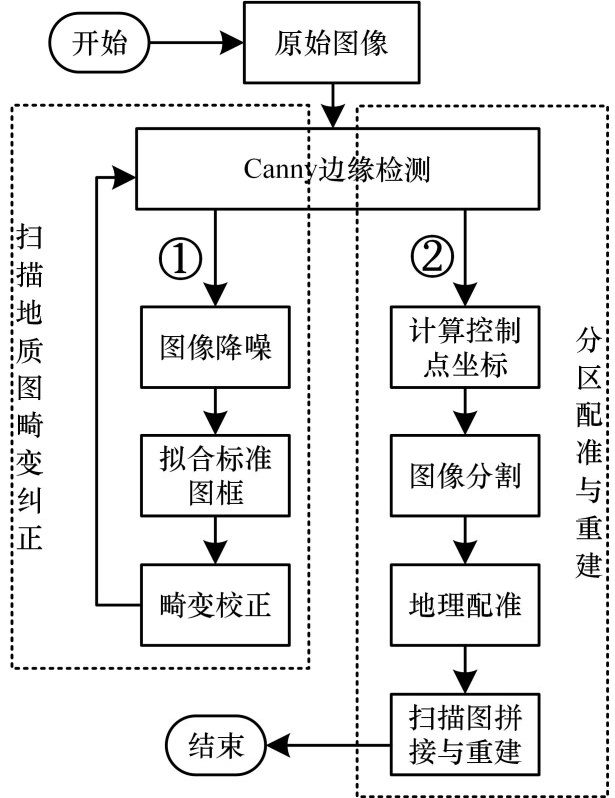
图2配准流程
对梯度计算的图像进行非极大值抑制然后采用双阈值法进行筛选标记,设置大阈值与小阈值,若像素梯度值大于阈值,则认为该像素是图像边缘;若小于小阈值,则排除该像素;处于大阈值与小阈值中间的判断其与已知边缘点是否连通,若连通则保留该点。最后将筛选出的所有边缘点相互连接得到图像边缘。
2.2 Bessel函数降噪与最小二乘拟合
将Canny变换得到的图廓线以10个像素为步长单位转为点要素,由于图廓线真值像素坐标是未知,以Bessel中误差为真值中误差,选择一倍中误差范围作置信区间对点要素进行降噪(邵建新, 2015);最后基于最小二乘法则拟合校正后图廓线 (图3)。

图3图廓拟合流程
2.3 畸变校正
根据2.2中拟合出的图廓,计算图廓网格点理论坐标,然后以图廓点为控制点采用一阶多项式变换对扫描图进行畸变校正。扫描图图廓边缘校正前后误差情况如图4所示,校正前横向图廓上的竖直图廓标识线存在明显偏移,图廓标识线位于理论位置(图4中黑线)两侧,校正后图廓线基本处于同一位置,偏差显著降低。

图4畸变校正前后图廓对比
a—边缘线降噪处理;b—理论图廓拟合
检查图像四周40个图廓点,畸变纠正前后坐标偏移情况(图5),计算图廓点平均偏差与水平方向、竖直方向图廓点拟合直线斜率(表1)。结果表明:校正后偏差减小,在20~35号点范围内,水平偏差、竖直偏差显著降低;校正后的误差拟合直线更为平缓,斜率趋近于0,各图廓点也围绕0误差线分布,说明畸变校在提高点位精度的同时保证了图像的几何完整性;校正后横向平均偏差、纵向平均偏差和总体偏差分别下降了52.90%、77.81%、69.26%,校正后各图廓点精度得到有效提升。
3 分区配准与重建
在扫描地质图中,变形情况和误差分布是不规律的,用统一的变换参数对全图进行转换会造成变换误差(马广彬等,2007;Diana and Shuhab,2019)。 Delaunay 三角网是一种经典的图像剖分算法,Delaunay三角网中任意三角形的外接圆范围内不包含其他点,任一控制点的点位偏差只会对其临近三角形产生影响,采用Delaunay三角网可以将纠正的范围控制在每个小三角形内使得变换函数能够反映出此范围的变换性质,有利于进行局部调整从而提高整体地理配准精度(周佳文等,2010;周雷等, 2019;Davood and Mohammad,2021)。Delaunay三角网建网关键步骤是选取三角形顶点,要求能够使畸变类型相近的区域划归为同一图形中。根据三角形所对应的变换函数参数逐一计算图形内每个点的真实地理坐标值。
表1畸变校正效果对比

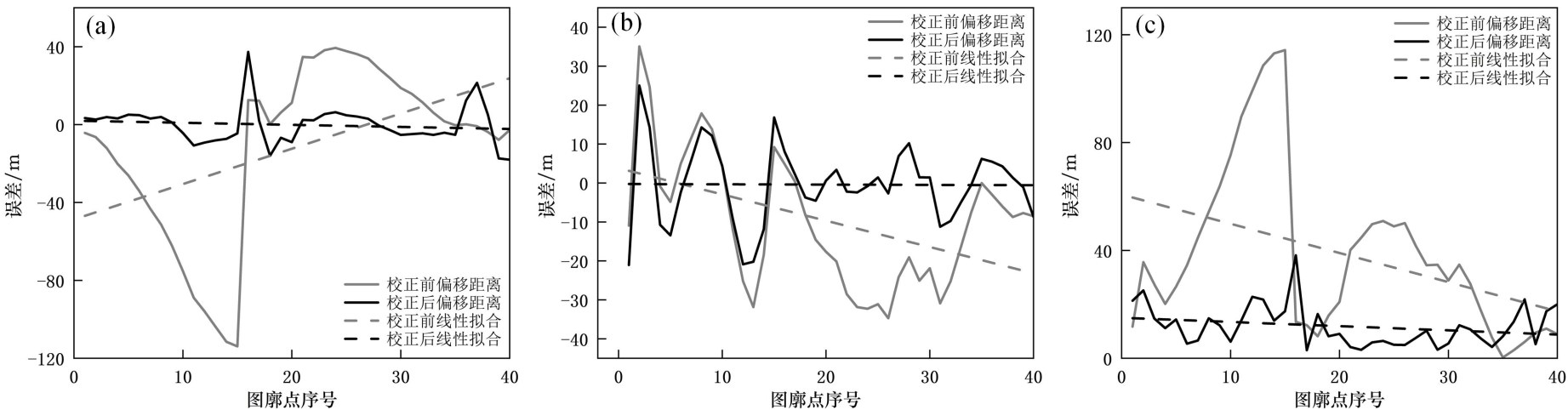
图5畸变校正前后图廓偏移量对比
a—竖直方向偏差;b—水平方向偏差;c—总偏差
本文以图廓点偏移方向延长线交点作为备选控制点,考虑图上已知坐标点分布与理论图廓格点位置,共选取31个三角形顶点构建Delaunay三角网 (图6)。
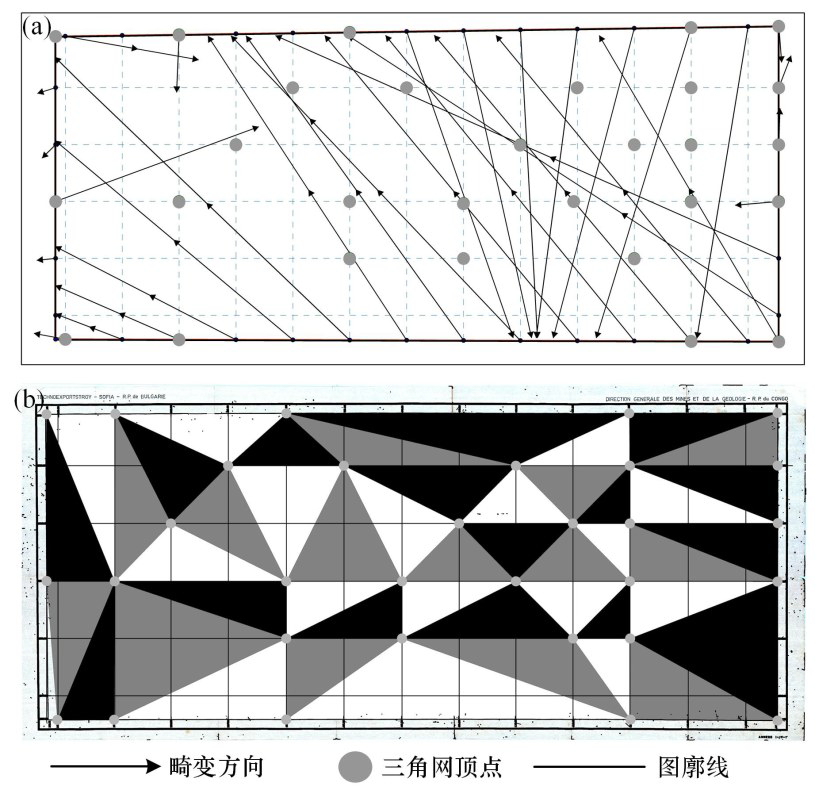
图6Delaunay三角网构建
a—原始图;b—生成三角网
实验将扫描地质图划分为51个三角形,最大的面积为106.95 km²,约占原地图总面积的6.24%,最小的面积为0.07 km²,约占原地图面积的0.004%。在这一阶段,每个三角形的图像覆盖范围相对有限,误差性质相似且经过了初步的校正,因此将扫描图由图像坐标系变换至地理坐标系这一过程主要涉及缩放、倾斜、旋转和平移,所以地理配准过程选择了仿射变换模型。
对畸变校正后的扫描地质图再次进行Canny边缘检测,解算控制点图上位置,利用三角网顶点坐标独立确定每个三角形的变换系数,然后对这些系数进行重构和组合得到完整配准后地图,完成扫描图像的整体精确地理配准。
4 图像地理配准精度评价
本节通过与目前常见的仿射变换模型、三阶多项式函数变换模型、样条函数变换模型的配准结果进行比较,来分析本文算法性能。评价指标使用图廓点配准精度、图内验证点(线)配准精度。
4.1 图廓点配准精度评价
实验使用40个图廓点,对比不同配准模型下的图廓点对的偏移结果,评价指标使用最大偏差、最小偏差、平均偏差、标准差,各模型图廓点地理配准精度如表2、表3所示。数据显示,本文模型在竖直方向平均偏差38.91 m,水平方向平均偏差52.24 m,竖直方向上平均偏差较相似多项式、仿射变换、三阶多项式、样条函数模型分别降低77.46%、67.93%、 45.50%、1.84%,水平方向上分别降低 79.20%、 66.28%、27.04%、23.98%,表明新方法离散程度小、整体几何精度更高。
此外,本文模型在竖直、水平方向上标准差分别为58.81、37.82,传统模型中竖直方向和水平方向图廓点配准标准差最小的是相似多项式模型与三阶多项式模型,标准差分别为64.25、39.64。这是由于本文模型在地理配准前已经进行了一次畸变校正,克服了图像自身变形影响,保证了图上要素配准后不变。
表2竖直方向图廓偏移比较
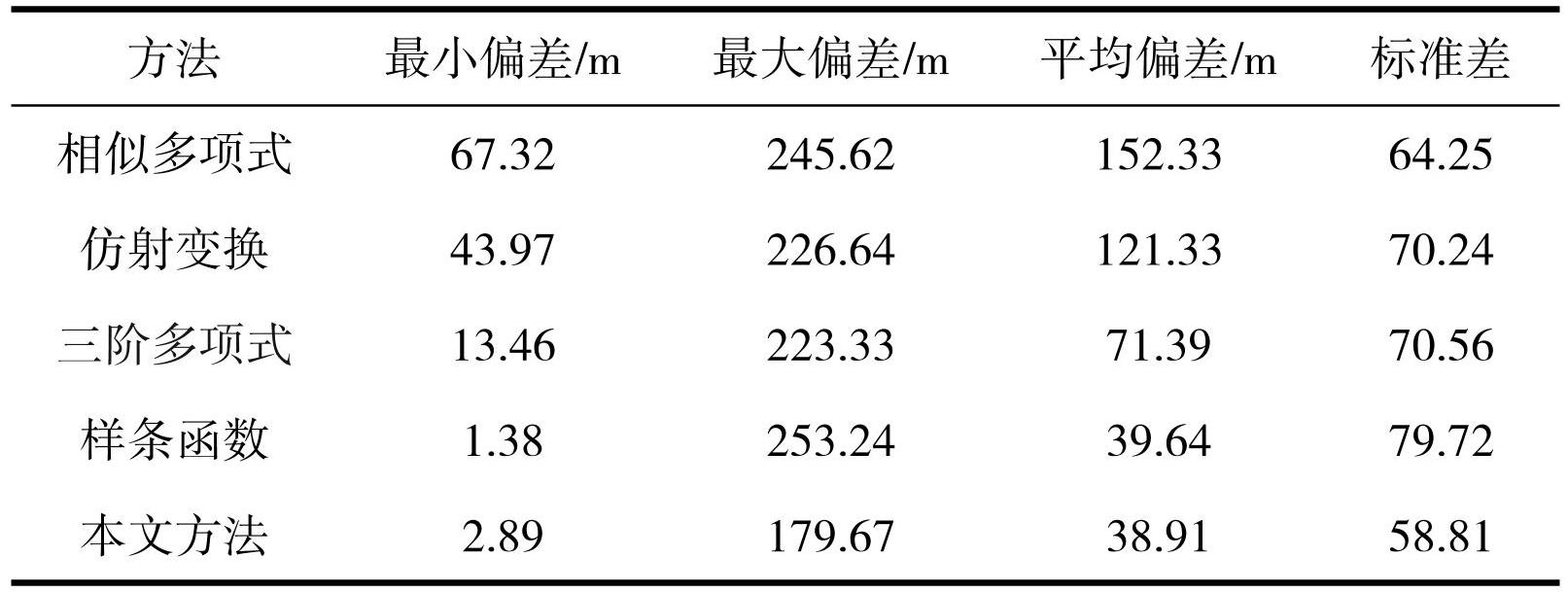
表3水平方向图廓偏移比较
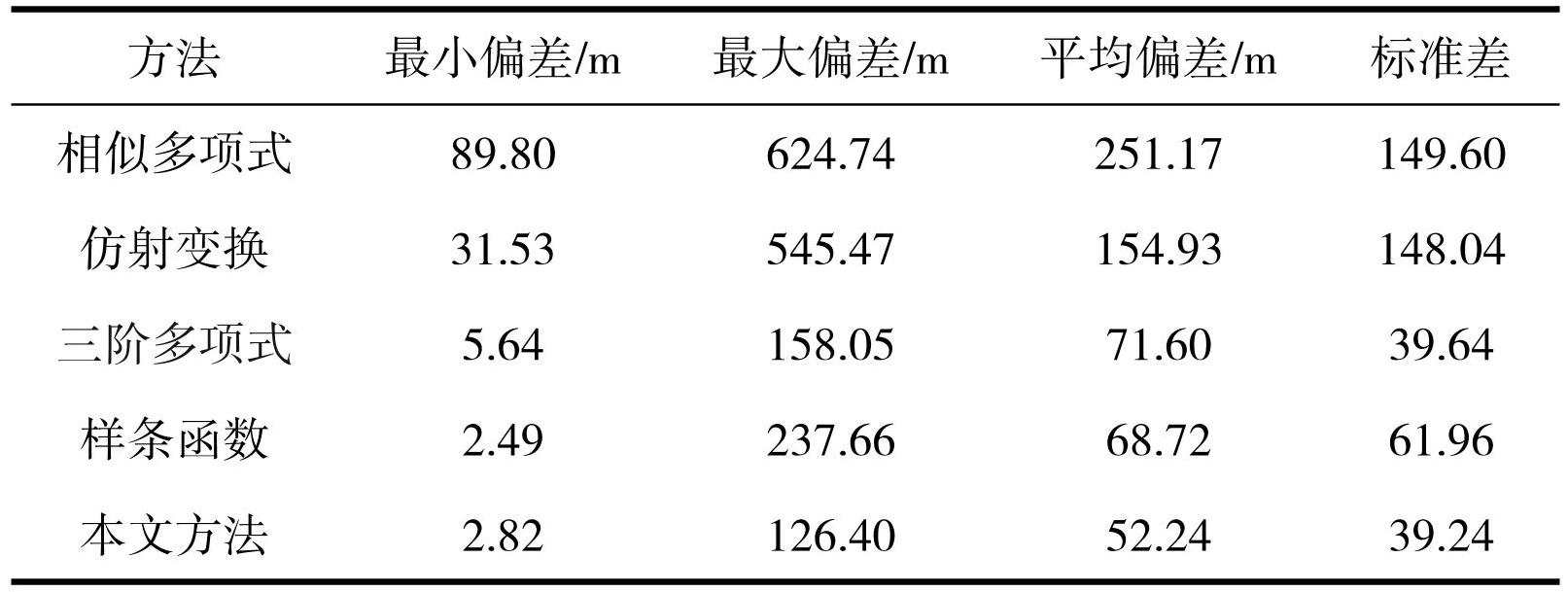
4.2 全图配准精度评价
从扫描地图和Sentinel-2A卫星图像中选取了具有代表性的评估区域,如图7所示,上排所示为 Sentinel-2A卫星图像与扫描地质图中的同名道路重合情况,下排为控制点图上位置与理论地理位置的偏移情况。结果表明:相似多项式模型与仿射变换模型配准中道路特征与其在Sentinel-2A卫星图像中的实际位置有较大的偏差,三阶多项式配准中线要素效果较好,但点要素配准误差仍较大,原因在于三阶多项式函数对全图求解最佳变换参数,可以校正复杂的图形变形,然而较三阶多项式容易出现外推误差,因此局部可能存在较大错位;样条函数配准中点要素效果较好,但该方法在对齐线性元素时会出现明显偏移,总体精度也较低,这是由于样条函数变换的性质,它是一种橡胶板变换方法,优先优化局部精度,而不是全局配准精度,表4进一步证实了这一观察结果,基于样条函数的地理配准验证点的最小偏差值最低,表明其在控制点附近的配准有效性。
本文配准模型下道路与参考影像上的相应道路紧密重合,验证点偏移情况与通过样条函数模型实现的结果非常接近,精度较高。这是因为本文方法在配准前首先对原始扫描图像进行了校正,有效地减轻了固有的图像失真;在地理配准阶段采用块校正策略来确定具有相似变形特征区域的配准参数,实现每一区域都是最佳配准参数。在保证几何配准精度的同时保证待配准影像内容的完整性,实现了高精度的地理配准。

图7配准效果示例
a—相似多项式;b—仿射变换;c—三阶多项式;d—样条函数;e—本文方法
1 —控制点图上位置;2—控制点理论位置;3—理论网格线
使用66个分布范围覆盖全图的精度验证点及经过几何精校正后的Sentinal-2A卫星影像上提取的扫描图同名线要素(共计79947 m),以最小偏差、最大偏差、平均偏差、召回率(点位误差小于两个栅格)、标准差、线要素重合率作为衡量指标对全幅图进行精度验证,结果见表4、表5。
表4验证点偏移情况统计
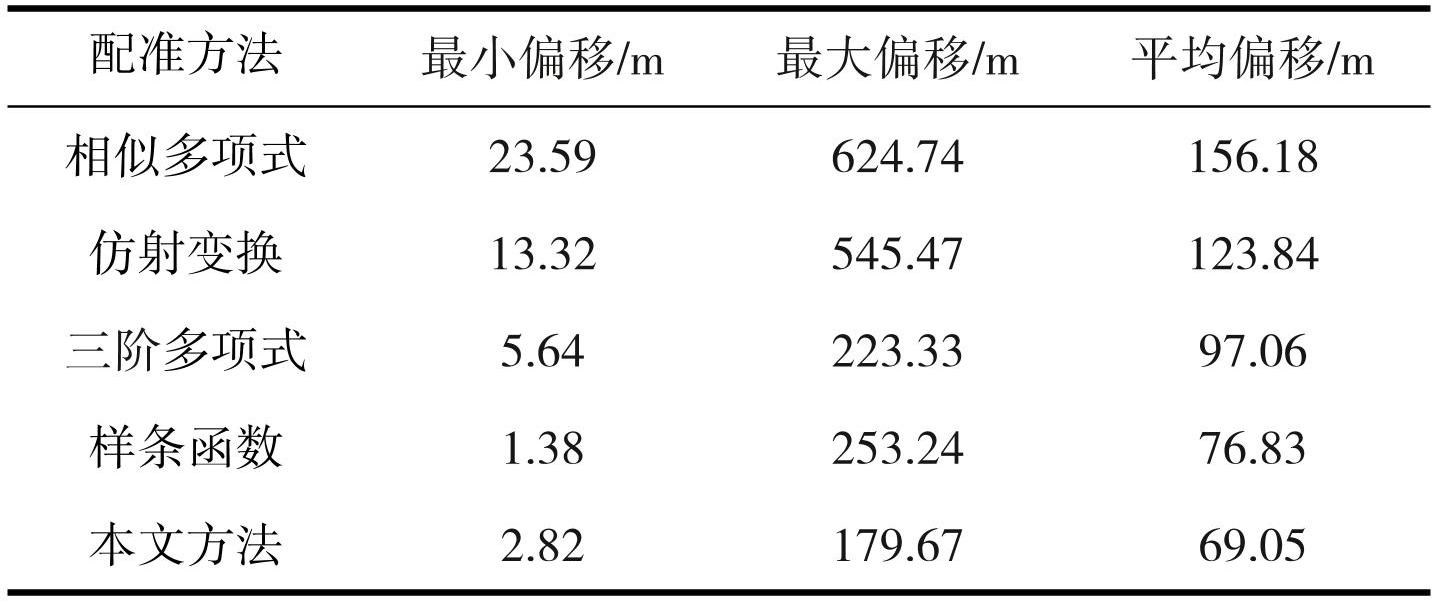
表5验证要素召回率情况统计

本文模型验证点平均距离偏差69.05 m、最小偏差2.82 m,其余模型中表现最好的是样条函数模型,其平均距离偏差76.83 m、最小偏差1.38 m。本文模型平均偏差较之提升了7.78 m,最小偏差略大,但这是由于样条函数具有优先控制点周围局部优化的性质。本文模型标准差为44.18,低于样条函数配准方法60.00的标准差,较传统方法中标准差最小的三阶多项式模型降低了15.82,表现出优秀的配准性能。
根据40个图廓验证点和26个图内验证点的偏差分布绘制成图8。4种传统模型中样条函数对控制点配准效果最佳,其分布曲线起伏平滑,没有明显的突变;三阶多项式函数配准效果次之,整体曲线变化稳定且偏移值较小;相似多项式和仿射变换模型的偏移值都有明显的波动,在10~15号、58~66 号、26和48号范围的验证区域内,误差急剧增加。这是因为传统的4种地理配准模型根据同一对地图计算校正系数。当扫描图像出现失真或地图尺寸较大时,求解出来的变换系数不能准确描述模型参数,而样条函数具有局部优化的性质,对异常区域有一定“分离”效果,图8的实验结果表明样条函数比其余传统配准模型对控制点的校正效果更好。
本文算法在地理配准阶段基于分区配准方法,依据变形情况采用Delaunay对扫描图进行剖分单独结算变换参数,从图8可以看出本文模型验证点曲线形状稳定且偏移距离处于较低值,在编号50~55验证点处偏移距离接近于0。统计精度验证点和验证线的召回率,从图8d可以看到本文配准方法点要素召回率和线要素重合率均最高,本文提出的新方法在拥有高配准精度的同时保证了图上内容不变性。
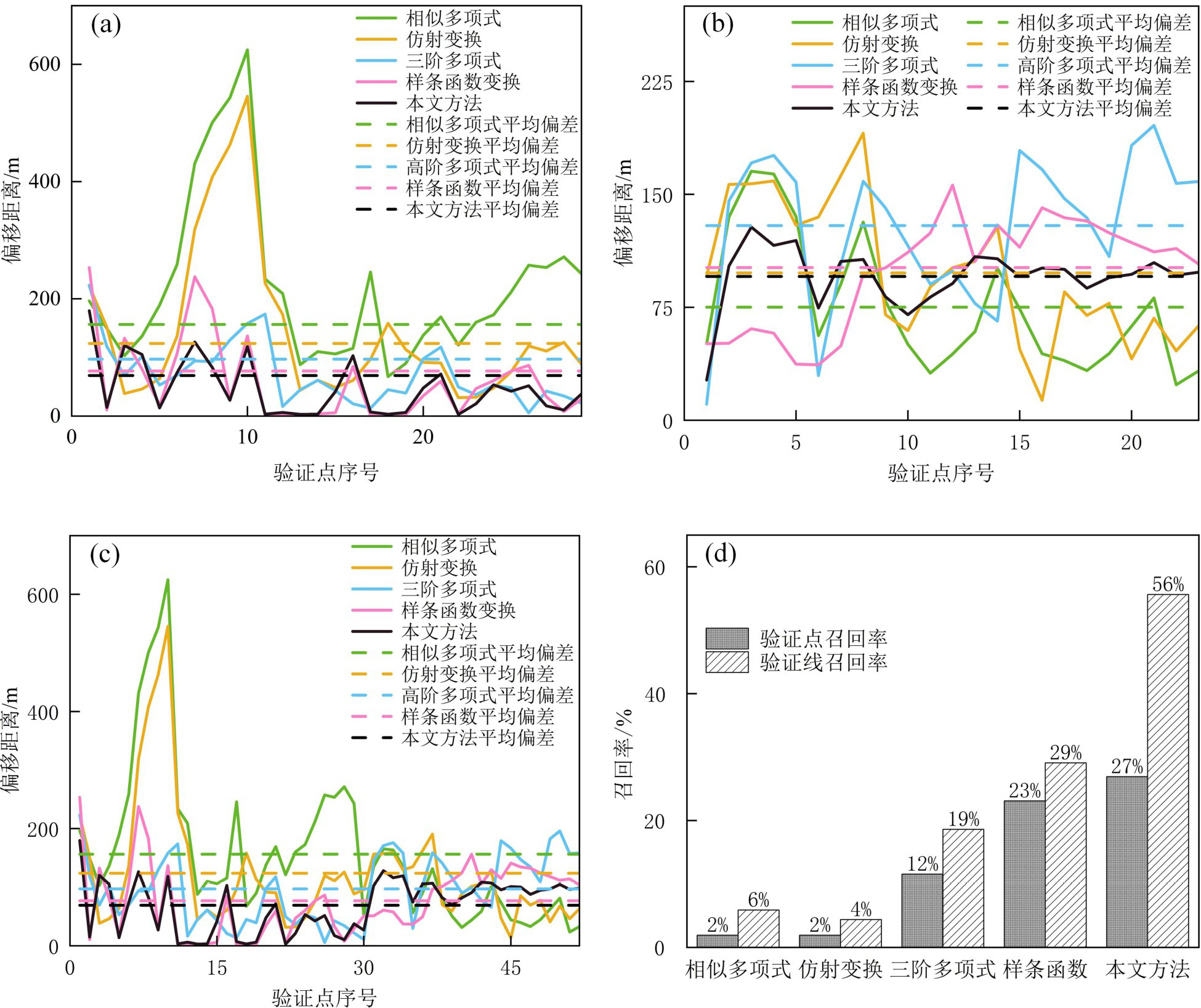
图8配准精度对比
a—图廓点误差分布;b—内部验证点误差分布;c—全体验证点误差分布;d—召回率对比
综合分析,传统4种配准模型中样条函数效果最好,其次是三阶多项式函数,表明当控制点数量与分布满足要求时,采用分区域配准的策略或更复杂的多项式模型可以有效纠正错综复杂的畸变。仿射变换主要对图像进行平移、缩放和旋转,而相似多项式保留了图形的形状,当原始图存在复杂畸变时这2种方法不能纠正图形扭曲,2种方法配准效果均不佳。与传统地理配准模型相比,本文提出的配准方法首先利用边缘检测算法对扫描图进行畸变校正,而后根据变形情况使用Delaunay三角网对图像进行分割,精细匹配后再重建得到配准结果。结果表明算法能显著提高图像配准质量,最终在保证图像变换鲁棒性的同时实现准确的地理配准。
5 结论
地理配准是指将扫描图像与地球表面的真实地理坐标系统进行对应的过程,以往的配准方法中大多忽视地图自身变形而直接对图像进行地理配准,难以实现存在复杂几何畸变的大图幅精确配准。本文提出一种边缘检测校正和分割配准相结合的扫描地质图配准算法,在顾及原始图自身畸变情况下实现精确几何配准,主要贡献如下:
(1)使用Canny算子和Bessel函数进行预处理,再由最小二乘法对图像进行畸变校正,有效降低了原始扫描图像存在的径向与切向畸变;
(2)使用Delaunay三角网根据变形程度分割图像,先分别求解配准模型转换参数,再重建完整图形,获得更为精确的地理配准地质图像;
(3)与传统基于相似多项式、仿射变换、三阶多项式、样条函数的配准方法相比,本文方法配准精度更高,实现了扫描地质图的高保真精确校正,有助于开展遥感地质解译、地球化学勘查、地球物理勘探等地质工作。
在未来工作中,还可更进一步探索配准步骤自动化及与其他多源异构地质数据的联合配准方法。












